ЧАСТЬ III.
ЧАСТЬ III.
ПИКСЕЛЬНАЯ ГРАФИКА
Глава 8. Разрешение пиксельной графики Глава 9. Глубина цвета пиксельной графики Глава 10. Объем файла пиксельной графики Глава 11. Трансформирование пиксельной графики
Данная часть является одной из главных и предлагает полное описание основ важного способа кодирования графической информации — пиксельной графики, при этом особенно выделено определение параметров пиксельной графики.
В данной части повторяются основные процессы на материале простого изображения, вывод основных параметров (разрешения и глубины цвета) и их единиц измерения, использование этих параметров для предварительного расчета объема файла и для трансформирования изображения пиксельной графики.
В главе 8 предлагаются дальнейшая конкретизация процедуры дискретизации и обсуждение важного параметра пиксельной графики — разрешения.
Глава 9 посвящена последующей конкретизации процедуры квантования и обсуждению важного параметра пиксельной графики — глубины цвета.
В главе 10 предлагается расчет объема пиксельного файла и обсуждение алгоритмов сжатия информации.
В главе 11 обсуждаются вопросы трансформирования пиксельной графики.
Пиксельная графика характеризуется тремя основными параметрами, один из которых совершенно очевиден (площадь изображения), а два других (разрешение и глубина цвета) требуют последовательного освоения материала.
Декартовы координаты
Декартовы координаты
Самый точный метод определения координат судна - это опрос местных жителей. Анекдот
Если мы договариваемся использовать в качестве дискретных элементов прямоугольники, то лучше декартовых координат трудно что-либо придумать. Действительно, из многих существующих координатных систем декартовы, названные по имени Рене Декарта, наиболее доступны и надежны для позиционирования на плоскости.
Поэтому самым простым способом разбиения плоскости представляются сетки, получаемые в пределах ортогональных (прямоугольных) координат.
Дискретизация штрихового изображения
Дискретизация штрихового изображения
- Как работает сканер?
- У-у-у...
Шутка
Итак, у нас все готово, чтобы начать конвертировать простейшее штриховое (черно-белое) изображение в цифровую форму. Предположим, нам очень повезло и необходимо превратить в цифровую форму такой "оригинал" -идеальный черный квадратик (рис. 7.3).
Эта глава является вводной перед
Глава 7.
Дискретизация, квантование и кодирование графических изображений
Эта глава является вводной перед обсуждением кодирования изображений, в ней пойдёт речь о процедурах, которые ранее относились к абстрактному сигналу, а теперь применяются к графическим изображениям.
В этой главе будет снова рассмотрен процесс дискретизации, но уже не в абстрактном изложении, а в применении к изображению, хотя и к простейшему.
Поскольку у изображения нет предварительного списка элементов, необходимо выполнить принудительную пространственную дискретизацию. Особенностью дискретизации изображений является двухмерность, что позволяет использовать для сохранения данных математический аппарат двумерных матриц. Именно для этого создается виртуальная матрица той же размерности по горизонтали и по вертикали, которая заполняется битами информации в соответствии с принятой заранее таблицей квантования.
Этим процессом заканчивается кодирование графического изображения. В результате формируется виртуальное цифровое изображение, которое для просмотра и управления требует особого этапа — визуализации. Необходимым условием визуализации является использование той же таблицы квантования, что и при оцифровке изображения.
Дискретизация, квантование...
ЧАСТЬ III ПИКСЕЛЬНАЯ ГРАФИКА Глава 7 Дискретизация, квантование и кодирование графических изображений Необходимость дискретизации изображений Характер дискретизации изображений Необходимость координат Декартовы координаты Дискретизация штрихового изображения Матрица дискретизации Квантование штрихового изображения Характер квантования изображения Таблица квантования для штрихового изображения Кодирование штрихового изображения Визуализация цифрового изображения Различие дискретизации и квантования Растеризация
Характер дискретизации изображений
Характер дискретизации изображений
Чтобы двигаться в нужном направлении, предварительно необходимо выяснить своеобразие графического сигнала, скажем, в сравнении с абстрактным сигналом, который выше уже обсуждался.
Информацию о работе с абстрактным аналоговым сигналом см. в части II.
Совершенно очевидно, что этот вопрос был поставлен только из соображений системности. Всякому, кто стремится войти в прекрасный мир изображений, понятно, что подавляющее число произведений традиционных направлений живописи, графики и фотографии располагаются на плоскости, соответственно, и все их содержательные элементы должны представлять какие-то плоскостные элементы: из совокупности площадей разной формы и цвета строится любое изображение.
Исходя из этого, способ дискретизации тоже должен основываться на плоских элементах, обладающих площадью, а, следовательно, двумя измерениями.
Кодирование штрихового изображения
Кодирование штрихового изображения
И я выхожу из пространства В запущенный сад величин.
Осип Мандельштам
И вот, наконец, мы начинаем кодировать исходное изображение ("оригинал") по двум состояниям, т. е. оценивать каждый дискретный элемент по составленной нами таблице квантования (табл. 7.1).
Там, где в "оригинале" дискретные ячейки имеют белый цвет, в соответствующие им ячейки матрицы (битовой карты) записываются "единицы". А там, где в "оригинале" представлены ячейки черного цвета, записываются "нули" (рис. 7.6).
| 1 |
1 |
1 |
1 |
||
| 1 |
0 |
0 |
1 |
||
| 1 |
0 |
0 |
1 |
||
| 1 |
1 |
1 |
1 |
||
| 1 |
1 |
1 |
1 |
||
Квантование штрихового изображения
Квантование штрихового изображения
Характер квантования изображения
После процедуры дискретизации наступает очередь следующего этапа — заполнения математической матрицы числовой информацией в соответствии с данными, фиксируемыми в пределах каждой ячейки дискретизации.
На предыдущем этапе изображение было принудительно "разрезано" на элементы ("квадратики") для того, чтобы отделить один элемент от другого. При этом каждый элемент получил свое уникальное положение в сетке дискретизации и, соответственно, в математической матрице.
Каждый отделенный элемент необходимо оценить в соответствии с некоторой заранее заданной шкалой — это и есть процедура квантования. Отличие данного процесса от того, который обсуждался ранее, состоит в характере квантования.
Информацию о понятии квантования см. в части II.
В изображениях (для начала ограничимся черно-белыми или тоновыми рисунками) единственное различие, которое имеет значение при таком типе дискретизации, строится на тональных градациях.
Матрица дискретизации
Матрица дискретизации
В самом деле, пока мы располагаем только страницей с рисунком (его мы самонадеянно окрестили "оригиналом"), на который нанесена сетка координат. Каким же образом эта информация преобразуется в цифровые данные и попадет в компьютер (например, в какое-либо графическое приложение)?
Необходимость дискретизации изображений
Необходимость дискретизации изображений
В общем случае полноцветное изображение (репродукция, цветная фотография, цветной слайд, а еще шире — прекрасная объективная реальность) представляет собой непрерывный (continuous) сигнал, не имеющий формально выраженных элементов (графического алфавита), которые можно было бы выделить, внести в список и поставить каждому цифровой код.
Эта тема подробно обсуждалась на примере буквенного алфавита в главе 3. Информацию об особенностях изображений см. в части II.
По этой причине понятно, что необходимо прибегнуть к "принудительной" дискретизации, как это было рассмотрено на примере абстрактного аналогового сигнала.
О работе с абстрактным аналоговым сигналом см. в части II.
В результате этой операции должны получиться некие дискретные элементы, которые можно подвергнуть операции квантования, а затем кодировать в соответствии с требуемой кодовой таблицей.
Необходимость координат
Необходимость координат
Зачем требуется однозначно позиционировать получаемые элементы, станет ясно после рассмотрения следующих ситуаций.
Определение
Матрица — это прямоугольная таблица из чисел (рис. 7.5) или математических выражений, состоящая из произвольного числа строк и столбцов. Каждая ячейка такой таблицы имеет одинаковый характер.
Определение
Битовая графика (bitmapped image) — это вид графики, у которого выполнена пространственная дискретизация и используются элементы, напоминающие элементы простейшей мозаики или вышивки крестом.
Но вот компьютерная матрица создана (она виртуальная, поскольку ее нельзя — пока! — увидеть). Теперь настала пора ее заполнить. Однако прежде необходимо разобраться, как это сделать, для чего нам требуется перейти к следующему этапу — квантованию.
Представьте себе обычную ситуацию: медсестра
Представьте себе обычную ситуацию: медсестра в палате измеряет температуру у больных и записывает показания термометра в специальную таблицу: 36,6; 37,2; 37,5; 38,4 и т. д. Казалось бы, фиксируется полная и вполне точная информация (как и положено, с точностью до одной десятой градуса).
И тем не менее любой из нас сообразит, что в этой таблице температур все-таки отражена не вся необходимая информация. Действительно, в таблице отсутствуют фамилии больных!
Без фамилий (или еще хуже: с неверно указанными фамилиями) такая таблица не только не имеет никакого смысла, но даже является вредной и опасной. На самом деле, эта таблица необходима и важна только в том случае, если обеспечивается однозначное соответствие значений, в данном случае — фамилий и значений температуры.
с целью определения магнитных аномалий.
Другой пример связан с геодезическими съемками, например с целью определения магнитных аномалий. Таблица значений уровней магнитного поля также будет бессмысленна, если не располагать точными координатами точек, в ко-
торых аномалия имеет место (под Курском или в центре Санкт-Петербурга). Не зря на профессиональном языке процесс определения координат и соответствующих им значений называется "привязкой" (location survey). В этом термине подчеркивается неотделимая связь значения и положения его на карте, а, соответственно, и в реальности.
Разумеется, что и дискретные элементы, на которые разбивается изображение, должны получить свое четкое местоположение. Следовательно, в этом случае требуются соответствующие координаты.
Растеризация
Растеризация
Процедура оцифровки изображения (дискретизации, квантования и кодирования) называется также растеризацией. Например, довольно часто это относится к преобразованию векторного изображения в пиксельное.
Полную информацию о преобразованиях векторной графики в пиксельную см. в части V.
Резюме
Параллельно в соответствии с количеством требуемых уровней тона (цвета) необходимо представить количество значений тона в виде таблицы квантования, или, другими словами, составить кодовую таблицу уровней тона (в данной главе использовались два тона). Каждому тону соответствует двоичный код.
Коды записываются в виртуальную (невидимую) математическую матрицу в соответствии со значением каждого дискретного элемента и сохраняются в одном из стандартных форматов.
И наконец, используя ту же кодовую таблицу, цифровое изображение в форме виртуальной матрицы выводят (визуализуют) на внешнее устройство, например монитор или принтер, теперь уже в форме, доступной для человеческого восприятия.
Весь цикл получения цифрового изображения простейшего "оригинала" — квадрата, нарисованного, например, черной тушью на белой бумаге, состоит из этапов дискретизации, квантования и кодирования. Для управления цифровым изображением или использования его в качестве графической информации необходимо обеспечить функцию визуализации.
Представив в целом процедуру оцифровки изображений в предыдущей главе, в последующих двух главах мы рассмотрим основные параметры пиксельной графики (а именно разрешение и глубину цвета), без понимания которых невозможно создать новое пиксельное изображение или правильно выполнить сканирование изображения, нанесенного на какой-либо материальный носитель (бумагу, картон, пленку и т. п.).
Различие дискретизации и квантования
Различие дискретизации и квантования
Хотя дискретизация и квантование основаны на едином принципе разбиения непрерывного сигнала на отдельные и независимые друг от друга элементы, необходимо провести четкую линию различия между ними.
В процессе квантования все одинаковые элементы необходимо разделить по какому-либо принципу хотя бы на "две кучки". Иначе никакого цифрового изображения получить нельзя: если все элементы будут иметь одно и то же значение, т. е. один и тот же цвет, получится элементарная плоскость ("плашка"), на которой отсутствует изобразительное содержание. Поэтому, для того, чтобы передать хоть какое-то содержание, мы должны научиться различать эти элементы в соответствии с предварительно заданной таблицей квантования.
Пример мозаики ("Дмитрий...
Рис. 7.1. Пример мозаики ("Дмитрий Солунский", мозаика начала XII века, Третьяковская галерея): дискретизация произвольная и адаптивная

Остается единственно возможное в этой ситуации решение — не пытаться искать в каждом отдельном изображении какие-то особые элементы (оставим это художникам), а наоборот, "навязать" всему огромному изобразительному корпусу свое простое, экономное и универсальное решение — принудительную дискретизацию (enforcement discretization) площади изображения на условные элементы одинаковой и максимально упрощенной формы (простой геометрической формы).
В данный момент ключевое слово - "принудительная". Дискретизация принудительна, т. к. никоим образом не учитывает содержание "картинки". Для принудительной дискретизации не играет роли, какую часть изображения мы "разбиваем" — фон или важные детали, часть рисунка или окружающие его поля и т. д. Если выразиться резко, то это — дискретизация "по живому" ("невзирая на лица").
Изображение в декартовых координатах
Рис. 7.2. Изображение в декартовых координатах
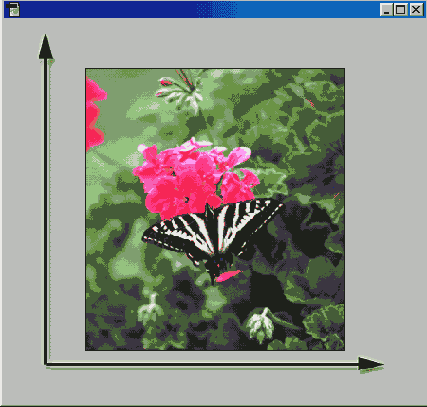
Простейший "оригинал"...
Рис. 7.3. Простейший "оригинал" для дискретизации (практически "Черный квадрат" Казимира Малевича)
Оригинал"...
Рис. 7.4. "Оригинал" в системе декартовых координат

Надеемся, вы согласитесь, что пока это еще не цифровое изображение, а в лучшем случае — подготовка к нему.
Пример математической матрицы
Рис. 7.5. Пример математической матрицы

Действительно, процедура дискретизации применительно к компьютерному изображению начинается с создания пустой матрицы, в ячейки которой можно записать числа — коды той или иной графической информации.
Осталось только поставить в жесткое и однозначное соответствие сетку дискретизации, которую мы нанесли на "оригинал", и математический объект — матрицу, которая виртуально создается средствами прикладных программ, например в оперативной памяти компьютера. В матрице фиксируется такое количество ячеек, которое достаточно для сохранения необходимого массива данных. А сетка дискретизации (декартовы координаты) -это, в общем, и есть таблица, или матрица.
Разумеется, с самого начала необходимо обеспечить идентичность размерностей: количество ячеек по горизонтали и по вертикали в сетке дискретизации должно соответствовать количеству строк и столбцов матрицы.
Заполнение виртуальной...
Рис. 7.6. Заполнение виртуальной матрицы битами, обозначающими коды цвета
После полного заполнения всех ячеек матрицы можно считать, что процесс оцифровки (кодирования) исходного изображения ("оригинала") завершился.
Битовая карта "оригинала"
Рис. 7.7. Битовая карта "оригинала"
Однако пользователю такая информация абсолютно не доступна. А для того чтобы управлять содержанием, например изменить какой-либо фрагмент изображения, необходимо выполнить процедуру, обратную вводу — визуализировать битовую карту, т. е. создать видимое изображение, в первую очередь на экране монитора.
Визуализированный "оттиск"
Рис. 7.8. Визуализированный "оттиск"

Те процессы, которые обсуждались выше на довольно абстрактном примере, сейчас рассмотрены на примере конкретного графического изображения (пусть и упрощенного). Действительно, на входе — конкретный "оригинал", на выходе — конкретный "оттиск".
Подробную информацию об абстрактном аналоговом примере см. в части II.
Справка
Характерным примером изображений, составленных из очевидно дискретных элементов, является мозаика, которая возникла в античную эпоху как элемент украшения зданий (рис. 7.1). Когда она создается (а это долгий и сложный в технологическом плане процесс), используются камни (смальта, керамические плитки) самых разных форм и размеров. Нет никаких принципиальных ограничений. Художник-мозаичист сам свободно выбирает камень, исходя из требуемого цвета и его площади ("каменного мазка"), т. е. учитываются, в первую очередь, содержание и творческая манера. В одном случае требуется камень большой площади, в другом — используются несколько мелких элементов.
О чем это говорит? Только о том, что для такой произвольной и очень гибкой дискретизации необходимы опыт, взгляд и рука художника. И даже, более того, желателен именно специалист по мозаике с достаточной практикой.
Для использования в технических системах указанный способ не может устроить, потому что он не технологичен. Тут требуется универсальный принцип, который можно было бы "поручить" электронному устройству.
Следовательно, нужно выбрать самый элементарный способ, а именно такой, который можно совершенно надежно алгоритмизировать и который всегда будет работать.
Справка
Координаты (от латинских слов "со", что означает "совместно" и "ordinates", что означает "упорядоченный" — это совокупность чисел, которые определяют положение точки на плоскости, на поверхности или в пространстве. Прямоугольные (декартовы) координаты точки на плоскости суть две взаимно перпендикулярные прямые, которые называются осями. Горизонтальная ось обычно обозначается буквой "X" и называется осью абсцисс, а вертикальная обозначается буквой "У" и называется осью ординат.
Информацию о других системах координат см. в главе 13.
Справка
Рене Декарт (1596—1650)— французский философ, математик, физик и физиолог. Положил начало аналитической геометрии, о которой мы, безусловно, вспомним в части, посвященной векторной графике. Декарт сформулировал закон сохранения количества движения, объяснил образование и движение небесных тел вихревыми потоками. Очень интересны философские взгляды Декарта, в частности он разделил душу и тело на две не связанные друг с другом категории, которые по причине божественного соизволения сосуществуют (правда, в разных пропорциях) только в человеке. Кроме того, Декарт — автор знаменитого высказывания "Cogito ergo sum", что означает "Мыслю, следовательно, существую".
По имени Декарта названа система координат на плоскости или в пространстве, обычно со взаимно перпендикулярными осями и одинаковыми масштабами по осям — так называемые "прямоугольные декартовы координаты".
Поэтому любое изображение (фотографию или рисунок) мы помещаем в декартовы координаты: по нижнему краю изображения располагается ось X, а с правым краем изображения совпадает ось Y.
В самом первом приближении элементы, на которые разбивается изображение, — это прямоугольные области. В общем случае образуются дискретные элементы с различными значениями ширины и высоты. Принципиально это не возбраняется, но, учитывая грядущие трансформации, стоит задуматься над тем, что даже ортогональные трансформации (вращение на 90, 180, 270 и 360 градусов) в такой ситуации будут чреваты неприятностями.
Более подробную информацию о неприятностях с трансформациями пиксельных изображений см. в главе 11.
Исходя из этих соображений, изображение выгодно разбивать на квадратные элементы.
А коль скоро принимаются за основу квадратные элементы, то и отсчеты на обеих осях устанавливаются одинаковыми, т. е. с равными интервалами между отсчетами (рис. 7.2).
Справка
Матрица используется во многих разделах физики, экономики и других точных науках, а в математике ею занимается так называемая матричная алгебра, описывающая правила и способы действия с матрицами. Следует заметить, что матрицы широко используются в компьютерных технологиях, поскольку любые устройства хранения информации можно трактовать как матрицу, каждая ячейка которой обладает определенным адресом (то есть координатами).
Справка
Например, в физике существует понятие "карта Карно" по расчету коэффициента полезного действия теплового двигателя. Такая карта, по сути, является обыкновенной таблицей.
В этом смысле карта (тар) — просто таблица, а поскольку в подобную таблицу записываются биты информации ("нули" или "единицы"), такая таблица (карта) получила название "битовая карта" (bitmap).
Подробную информацию о понятии "бит" см. в части II.
В связи с этим дискретную компьютерную графику иногда называют "битовой" (bitmapped).
Таблица квантования
Таблица квантования
для штрихового изображения
Поскольку в штриховом изображении используются только два ахроматических цвета, их можно представить как два состояния. Выше мы обсуждали: для того, чтобы закодировать два состояния, требуется всего один двоичный разряд (один бит информации).
Подробнее о построении кодовой таблицы см. в части II.
На основании этого мы можем предварительно составить таблицу квантования для штрихового изображения (табл. 7.1).
Таблица 7.1. Таблица квантования для штрихового изображения
| Значение ахроматического цвета |
Коды (1 двоичный разряд) |
||
| Черный Белый |
0 1 |
||
Важная мысль
Математическая матрица, заполненная совокупностью цифр (кодов), — это по сути и есть изображение в цифровом виде, т. е. цифровое изображение.
Таким образом, полученная таблица (битовая карта) (рис. 7.7) может быть записана любым компьютерным способом как последовательность двоичных чисел, импульсов, положения магнитных доменов и т. д. В таком виде информацию можно хранить (в одном из стандартных форматов), передавать, в том числе копировать неограниченное число раз и вообще обрабатывать средствами вычислительных систем.
| 1 |
1 |
1 |
1 |
||
| 1 |
0 |
0 |
1 |
||
| 1 |
0 |
0 |
1 |
||
| 1 |
1 |
1 |
1 |
||
| 1 |
1 |
1 |
1 |
||
Важная мысль
Для преобразования изображений в цифровую форму первым условием также является "принудительная" дискретизация.
А пока, исходя из того, что у графики нет явно выраженных (и самое главное — универсальных) элементов, можно констатировать принципиальную исходную позицию: изображение необходимо подвергнуть дискретизации, но прежде следует ответить на довольно простой вопрос: каков характер предстоящей дискретизации.
Важная мысль
Принудительная дискретизация изображений позволяет создать универсальный способ создания элементов для последующего квантования и кодирования.
Таким образом, принудительная дискретизация позволяет решить поставленную выше задачу легко и изящно. В простоте этого метода кроется огромный запас "жизненной силы" и одно из главных его достоинств. Но вместе с тем, как всегда в жизни, главное достоинство является причиной очень многих огорчений, связанных с этим методом.
Подробную информацию о "плюсах" и "минусах" этого метода см. в части V.
Вторым по важности ключевым словом является "простой", т. е. речь в данном случае идет о том, что необходимо выбрать самый простой элемент дискретизации. А что может быть проще "квадратика"?! (Только линия, которая, как мы выяснили, для реализации этой задачи не подходит.)
При этом, правда, неизбежно возникают следующие вопросы.
Содержательный вопрос: как описать фактическое различие между элементами?
Формальный вопрос решается введением координатной сетки, а содержательный — последующим этапом квантования.
Информацию о координатной сетке см, в следующем разделе, а о квантовании — в разд. "Квантование штрихового изображения" данной главы.
Важная мысль
Для изображений идеально подходит дискретизация на квадратные элементы, положение которых однозначно определяется по декартовой системе координат.
Важная мысль
Здесь собственно и начинается то, что мы называем компьютерной графикой, ибо с этого момента мы переходим к представлению информации средствами компьютера, т. е. цифрами.
А из цифр, если они характеризуют некий ареал значений, как правило, можно составить таблицу, которая на математическом языке называется матрицей.
Важная мысль
Размерность сетки дискретизации "оригинала" должна соответствовать размерности виртуальной цифровой матрицы.
Следует только добавить, что матрица, которая создается средствами графической программы, получила в английской терминологии название тар ("карта").
Важная мысль
Характер квантования дискретных элементов изображений состоит в различении элементов по уровню освещенности (по уровню тона).
Визуализация цифрового изображения
Визуализация цифрового изображения
На данном этапе цифровое изображение ("скрытое изображение") получило форму, доступную для хранения и обработки на соответствующих электронных устройствах, но недоступную для восприятия и управления человеком.
Для того чтобы эту ситуацию исправить, мы должны заставить программу и соответствующие драйверы устройств, используя ту же самую таблицу квантования (табл. 7.1), полученную матрицу (рис. 7.7) представить доступными для человеческого восприятия средствами — визуализировать цифровое изображение, например на экране монитора (хотя, в конечном счете, не окажется лишним и принтер).
В общем случае получается некий "оттиск" (рис. 7.8) — конечный продукт, который мы получаем с использованием технического устройства.
в кавычки по той же
Заметьте, что слово "оттиск" помещено в кавычки по той же причине, что и "оригинал".
И заметно, что в общем и целом "оригинал" похож на "оттиск". Это значит, что общими усилиями мы справились с задачей и правильно прошли все требуемые этапы.
в том, что многие читатели
Мы отдаем себе отчет в том, что многие читатели уже используют в своей работе сканирующие устройства с большим или меньшим успехом... Однако следует сразу понять, что мы начнем обсуждать не техническую, а только логическую сторону этих процессов, а именно рассмотрим только самые общие принципы, на которых основано огромное множество указанных устройств. Если читателей интересуют именно конкретные технические вопросы, они могут параллельно обратиться к книгам издательства БХВ-Петербург: "Сканеры и цифровые камеры".
В каких случаях нам достаточно
В каких случаях нам достаточно одной линейной дискретизации? Конечно, когда, нужно выяснить размер с помощью измерительного устройства типа "линейка": линейка снабжается дискретными отметками.
В этом случае необходимо плоскостное изображение дискретизировать на какие-то плоские элементы, обладающие параметрами площади, т. е. длиной и шириной.
Какую форму могут (или должны) иметь дискретные элементы в самом общем случае? В принципе, любую.
в кавычки, потому что это
Мы будем использовать понятие "оригинал", но берем это слово в кавычки, потому что это пока условный, очень упрощенный рисунок — некая модель изображения.
Если вы знакомы с предыдущими частями этой книги, для вас будет естественным предположить, что первым этапом нашей работы является дискретизация?
работу сканер, когда перед ним
Мы говорим в данном случае о том, с чего теоретически "начнет" работу сканер, когда перед ним "ставится" задача — превратить графическое изображение в цифровую форму.
Мы помещаем "оригинал" в декартовы координаты, а фактически — просто строим сетку, линии которой образуют клетки-ячейки, т. е. независимые друг от друга дискретные элементы (если выразиться короче — "дискреты").
На изображении получаются дискретные элементы по вертикали, которые можно, например, пронумеровать и дискретные элементы по горизонтали, которым, также можно поставить в соответствие такую же систему обозначений (рис. 7.4).
Забегая вперед, можно сказать, что
Забегая вперед, можно сказать, что это справедливо даже для квантования цветных изображений.
Вспомним, что мы выбрали для экспериментов черно-белый штриховой "оригинал". "Штриховой" означает, что используется жесткая дихотомия: либо одно, либо другое, т. е. только белое или только черное. Это послужит путеводной нитью в составлении таблицы квантования.