Анимация

Возможно, что для новичков в ЗD-проектировании способность анимиро-вать любые изменения параметров объектов, их положения и ориентации в пространстве, свойств их материалов является самой удивительной и потрясающей воображение особенностью.

Базовым принципом компьютерной анимации (как, собственно говоря, и любой другой) является быстрая смена последовательности кадров (frames), фиксирующих промежуточные фазы движения, перед глазами наблюдателя.

Под движением подразумевается как непосредственно перемещение или поворот объекта в пространстве сцены, так и любое изменение его формы, цвета и т. п. Кадры должны сменять друг друга при просмотре с достаточно высокой скоростью, иначе у наблюдателя не создастся иллюзии непрерывности происходящих изменений.

Обычно частота воспроизведения кадров (film rate) не должна быть ниже 12 кадров в секунду (frame per second, fps). При выборе той или иной целевой платформы важно правильно выбрать покадровую частоту анимации. Так, кинематограф работает с частотой 24 кадра в секунду, в телевизионных форматах PAL/SECAM и NTSC частота кадров равняется 25 и 30 соответственно.

Большинство анимационных программ реализуют метод ключевой анимации (keyframe animation) объектов, заимствованный из традиционной мультипликации. Суть этого метода состоит в разделении кадров на ключевые (keyframes) и промежуточные (tweens). В ключевых кадрах художник-аниматор фиксирует ключевые (критически важные, опорные) фазы анимации объекта, например положение спортсмена непосредственно перед прыжком или верхнюю точку полета волейбольного мяча. В промежуточных кадрах сама программа интерполирует остальные фазы анимации объекта, используя при этом дополнительную информацию, полученную от аниматора. Таким образом, задавая ключевые кадры для параметров объекта и определяя типы интерполяции между ними (линейная, скачкообразная, с ускорением и т. п.), мы получаем в свое распоряжение очень простой и достаточно мощный анимационный инструментарий.

С другой стороны, ключевая анимация не всегда является оптимальным выбором. Например, если необходимо "заставить" объект совершить сложный пируэт в пространстве, то, наверное, проще нарисовать для него нужную сплайновую траекторию, чем определять десятки (а то и сотни!) ключевых кадров. Такая, не требующая задания большого количества ключевых кадров, анимация называется параметрической (parametric animation). Обычно она реализована как набор предустановленных анимационных эффектов, plug-in-модулей, например случайного изменения параметра или движения по траектории. Достаточно задать время начала и завершения такого эффекта, настроить его параметры, а обо всем остальном позаботится анимационная программа.

Цвет

Выбирая цвет материала, необходимо ответить на следующие вопросы.

Какой у материала цветовой тон (hue), т. е. какого собственно цвета (красного, зеленого или какого-либо другого)?
Какая у него насыщенность (saturation), т. е. как сильно окрашен отраженный свет? Высокая насыщенность делает цвета более глубокими (deepen), а меньшая насыщенность ведет к исключению цвета (переход к ахроматическим цветам).
Какова его яркость (value), т. е. как много света отражает материал? Этот параметр влияет также на характеристику зеркальности поверхности.

Кроме модели цвета HSV, которая практически не характерна для пиксельной графики, могут использоваться цветовая модель RGB или файл с текстурной картой (texture map).

Дополнительные свойства материалов

В зависимости от конкретной программы трехмерного моделирования предлагается различная совокупность дополнительных свойств материалов. Например, пакет 3D Studio MAX позволяет моделировать динамику твердых тел (dynamics of rigid bodies), что приводит в этом случае к необходимости задать коэффиент упругости материала (bounce coefficient) и коэффициенты силы трения покоя (static friction) и трения скольжения (sliding friction).

Геометрические объекты

Весьма проблематично в кратком обзоре возможностей трехмерной графики исчерпывающе рассказать обо всем многообразии инструментов моделирования, используемых в различных программах. Поэтому оставляем за собой право выбрать один из самых распространенных и мощных ЗВ-пакетов и на его примере обсудить основные типы объектов и технологии их моделирования. В качестве референтной программы ЗВ-моделирования и анимации был выбран уже упоминаемый пакет 3D Studio MAX компании Discreet.

Вот краткий перечень типов геометрических объектов, которые могут быть созданы в этой программе.

Сплайновые кривые (spline curves) (рис. 13.4) — это смоделированные таким образом кривые (Безье или NURBS), что они могут служить заготовками для построения поверхностей (экструзии, тела вращения или лоф-тинга) или их можно использовать в качестве траектории движения. Для кривых Безье определен, в частности, набор примитивов (например, окружность или текст), которые впоследствии могут быть конвертированы в явное ("повершинное") описание формы. При отображении на экране и при финальной визуализации кривые аппроксимируются линейными отрезками с заданной точностью.

Данная глава представляет краткую информацию

Глава 13.

Трехмерная графика

Данная глава представляет краткую информацию об очень сложном и многообразном направлении цифровой векторной графики — трехмерной графике.

Трехмерная графика характеризуется многоаспектной интеграцией: пользователю необходимо обладать знаниями в областях проектирования, освещения, перемещения объектов и камер, декорирования объемных моделей, использования звуковых и визуальных эффектов, сценарных и покадровых разработок, не считая чисто технических сложностей.

В силу такой специфики трехмерной графики (а именно ее чрезвычайной сложности) данная глава стоит особняком: в ней представлена только краткая информация о составляющих элементах этой области: пространствах, моделировании объектов, их текстурировании, анимации, освещении и визуализации.

Трехмерная графика

Глава 13 Трехмерная графика Специфика трехмерной графики Рабочее пространство Системы координат Типы пространств Моделирование объектов Геометрические объекты Негеометрические объекты Материалы и карты Цвет Прозрачность Глянцевость Коэффициент преломления Корректное моделирование материалов Текстурирование материалов Управление текстурированием Дополнительные свойства материалов Анимация Визуализация Локальное освещение Глобальное освещение

Глобальное освещение

Однако алгоритмы локального освещения не позволяют получать корректные итоговые изображения, т. к. не учитывают более сложные взаимодействия поверхностей и освещения сцены. Вот только некоторые из них:

поверхности могут блокировать часть падающего на них света и отбрасывать тени на другие поверхности;
в блестящих поверхностях могут присутствовать отражения других объектов;
на поверхностях могут возникать рефлексы;
прозрачные поверхности позволяют видеть объекты, находящиеся за ними.

Алгоритмы просчета глобального освещения при визуализации корректно учитывают прохождение света между поверхностями, что решает поставленные проблемы. Чаще всего используются два таких алгоритма:

трассирование лучей (ray tracing); излучательность (radiosity).

Алгоритм трассирования лучей отслеживает в обратном направлении (backward) прохождение лучей света от глаза наблюдателя через каждый пиксел итогового изображения к поверхностям визуализируемых объектов. В случае пересечения трассируемого луча с поверхностью происходит одна из следующих ситуаций.

Если поверхность не зеркальная и не прозрачная, за ней образуется тень. Цвет самой поверхности в точке пересечения вычисляется с учетом характеристик источников освещения.
Для зеркальных поверхностей делается оценка дальнейшего прохождения отраженного света (reflected light).
Для прозрачных — пропущенного света (transmitted light).

В последних двух случаях оценка дальнейшего прохождения луча повторяется при последующих пересечениях с поверхностями, но не более определенного количества раз (итераций).

Алгоритм обратного трассирования лучей является очень мощным и гибким. Он позволяет аккуратно просчитывать такие характеристики глобального освещения, как тени, зеркальные отражения, преломления света в прозрачных материалах.

Однако он имеет два существенных недостатка:

высокая сложность и, как следствие, малая скорость вычислений;
подмена просчитанного непрямого освещения (indirect lighting) на "абстрактный" окружающий свет (ambient light), что приводит, например, к отсутствию рефлексов на поверхностях.

Алгоритм просчета излучательности фундаментально отличается от алгоритма трассирования лучей. Вместо вычисления цвета каждого пиксела итогового изображения этот алгоритм просчитывает интенсивность каждой точки пространства сцены. Поверхности всех объектов разбиваются на элементы (небольшие по площади) и для каждого из них вычисляется, сколько света он излучает на остальные элементы. Этот алгоритм, изобретенный в 1960-х годах, был значительно модернизирован в 1988 году и получил название алгоритма излучательности с последовательной детализацией (progressive refinement radiosity). Это новшество означает, что мы сможем наблюдать за улучшением качества и детализации изображения при прогрессивном разбиении поверхностей на более мелкие элементы.

Полученное таким образом изображение сцены является корректным с точки зрения отражений света между поверхностями (diffuse interreflections), но имеет и свои неустранимые недостатки:

большие затраты памяти при вычислениях;
отсутствие в полученном изображении отражений и преломлений света в прозрачных поверхностях.

Так как ни один из вышеизложенных алгоритмов не может полностью решить проблему корректного вычисления глобального освещения, в профессиональных пакетах 3D-визуализации они используются совместно. Примером удачного сочетания этих алгоритмов для финальной визуализации может служить уже упоминавшаяся программа Lightscape.

Резюме

В силу специфики 3D-моделирования и возможности работать с анимацией (отображения изображений во временном развитии) такие программы занимают особое место в линейке графических программ.
Пакеты трехмерной графики предъявляют повышенные требования как к аппаратно-программным средствам используемого компьютера, так и к уровню знаний работающего с ними дизайнера.
Идея векторной графики состоит в описании линейных фрагментов с помошью единственной формулы.
При этом разбиение произвольных кривых на отдельные фрагменты (сегменты) разумно выполнять, учитывая следующие исходные условия: фрагменты должны быть достаточно короткими, а формула должна обеспечивать достаточно близкую аппроксимацию кривых.
Линейная зависимость обладает важным достоинством — простотой, но при этом не лишена серьезных недостатков (объекты, составленные только из прямолинейных сегментов, лишаются возможности произвольного масштабирования, для достоверной аппроксимации формы объекта потребуются десятки тысяч линейных сегментов).
Поэтому неизбежной заменой прямолинейных сегментов могут быть только кривые, которые способны обеспечить требуемую гладкость (речь идет о кривых Безье и NURBS-кривых).
Если обращаться к уравнениям со степенью выше первой, следует признать, что явный способ представления не может применяться там, где требуется описание произвольных кривых, размещаемых в произвольных местах на плоскости.
Альтернативным способом описания кривой является определение кривой как параметрической сплайновой функции.
Одной из основополагающих особенностей NURBS-кривой является то, что ее форма определяется расположением множества контрольных точек (control points). Она позволяет локализовать изменение формы кривой перемещением отдельных контрольных точек без изменения формы всей кривой в целом.
Рациональные кривые обладают двумя дополнительными свойствами (они обеспечивают корректный результат при проекционных трансформациях (например, масштабировании), их можно использовать для моделирования кривых любого вида, включая конические сечения).
При всех своих выдающихся свойствах NURBS-кривые все же обладают существенным недостатком: расширенные возможности не могли не сказаться на сложности и на уровне инструментария для их построения, а это, в свою очередь, требует от дизайнера повышенных условий для его освоения, не говоря уже о необходимости определенного уровня математической подготовки.
Кривые Безье получили широкое распространение, т. к. обладают следующими важными свойствами (начальная и конечная контрольные точки лежат на кривой, кривая на всем протяжении непрерывна, у нее отсутствуют разрывы, касательные к кривой в начальной и конечной контрольных точках являются отрезками, соединяющими их с двумя другими соседними контрольными точками).
Для построения кривой Безье требуются четыре контрольных точки, хотя кривая физически проходит только через две из них (опорные точки). Две точки остаются в стороне (управляющие точки).
Соединительные точки между сегментами бывают нескольких типов, что позволяет обеспечивать различные формы соединения (гладкую, тангенциальную или на изгиб).
Язык описания страницы PostScript, созданный как язык управления графическими устройствами, решает задачи по передаче информации между прикладными программами (графическими редакторами, программами верстки) и устройствами визуализации (лазерными принтерами, фотонаборными автоматами и цифровыми офсетными машинами).
Последующее развитие языка PostScript не изменило своей основы и продолжает идти по пути интегрирования новых возможностей выводных устройств (цветная печать, системы управления цветом и т. д.).
Каждая векторная программа обладает собственным графическим форматом, между этими форматами нет однозначного соответствия, поэтому конвертирование одного формата в другой сопряжено с многочисленными погрешностями, особенно в последнее время, когда векторные программы насыщены разнообразными эффектами.
В силу специфики 3D-моделирования и возможности работать с анимацией (отображения изображений во временном развитии) такие программы занимают особое место в линейке графических программ.
Пакеты трехмерной графики предъявляют повышенные требования как к аппаратно-программным средствам используемого компьютера, так и к уровню знаний работающего с ними дизайнера.

Часть III была посвящена исключительно пиксельной графике, а часть IV— исключительно векторной графике, которая при всей своей сложности обладает массой достоинств, хотя она и не лишена недостатков. О достоинствах и недостатках пиксельной и векторной графики, а также об их взаимных преобразованиях повествует следующая часть.

Глянцевость

Глянцевость материала определяет характерный вид отражении и оликов на поверхности объекта. При визуализации на материалах с высокой глянцевостью будут получены более четкие зеркальные отражения и более резкие блики.

Коэффициент преломления

Коэффициент преломления определяет характер изменения света при прохождении им границы между двумя разными средами (обычно каким-нибудь материалом и воздухом).

Эта характеристика влияет на силу бликовости материала или, в случае прозрачных материалов (например, воды или стекла), на величину искривления (преломления) формы объектов, находящихся сзади.

Если коэффициент преломления равен 1, падающий свет без потерь (отражений) проникает в материал. Для непрозрачного объекта это означает, что его поверхность будет выглядеть абсолютно матовой, для прозрачного, что преломления будут отсутствовать.

Корректное моделирование материалов

Важно помнить, что для получения финальной визуализации фотореалистического качества нужно, помимо прочего, очень корректно задавать свойства материала. В программе Lightscape это помогают сделать шаблоны материалов (material templates) с различными физическими свойствами.

Использование таких шаблонов резко ускорит работу и избавит от большинства глупых ошибок (например, металл никогда не окажется прозрачным).

Локальное освещение

Алгоритмы локального освещения описывают то, как каждая поверхность отражает или пропускает свет. Эти математические алгоритмы вычисляют интенсивность, цвет и дальнейшее (после отражения или прохождения насквозь) распределение света, упавшего на поверхность объекта. Простейшие из таких алгоритмов рассматривают только свет, непосредственно пришедший от источников освещения к тонируемой поверхности.

Материалы и карты

Материалы определяют визуальные свойства поверхностей, т. е. описывают то, как поверхность объекта взаимодействует с освещением сцены. Различные программы используют разные наборы параметров описания свойств материалов. В качестве примера для данного случая можно рассмотреть пакет Lightscape (фирмы Autodesk, Inc.). В частности, в нем замечательно реализовано описание характеристик материала. Выбор "образцовой" программы обусловлен тем, что она является одной из немногих, где используется физически корректная технология моделирования материалов.

Следующие свойства поверхностей определяют взаимодействие материала со светом:

цвет (color);
прозрачность (transparency);
глянцевость (shininess);
коэффициент преломления (refractive index).

Цвет и прозрачность определяют прямое (direct) и непрямое (indirect) рассеянное освещение (diffuse lighting), вычисляемое при итоговой визуализации с помощью алгоритма излучательности (radiosity).

Коэффициент преломления и глянцевость (полированность) материала определяют блики (highlights) и зеркальные отражения (specular reflections) на поверхности. Блики и отражения просчитываются при визуализации с помощью алгоритма трассировки лучей (ray tracing).

Моделирование объектов

В первом приближении все создаваемые трехмерные объекты можно разделить на геометрические и негеометрические.

Первые из них используются для моделирования фактической "начинки" сцены: персонажей, предметов, другими словами, — объектов вещественного мира.
Вторые же применяются для придания сцене реалистичности (скажем, правильного освещения), для, моделирования физических сил, действующих на объекты (например, гравитации или порывов ветра), для реализации других утилитарных целей (например, повышения точности построений, измерения расстояний и т. п.).

Другими словами, геометрические объекты будут присутствовать в визуализированном кадре явно (как кривые или поверхности), а негеометрические — опосредствованно (в виде бликов, теней, ускорений и т. п.). .

Негеометрические объекты

Продолжая рассматривать программу 3D Studio MAX в качестве примера, кратко опишем инструментарий создания негеометрических объектов. Внимания заслуживают следующие типы объектов.

Источники света (light objects) (рис. 13.11) используются при моделировании наружного (exterior) и интерьерного (interior) освещения. Различные типы источников реализуют различные алгоритмы распространения света: всенаправленные лучи из точечного источника (omni light); сфокусированный луч из прожекторного источника (spotlight); параллельные лучи из направленного источника (direct light). Кстати, последний тип чаще всего используется при моделировании солнечного света (sunlight). При этом испускаемый источниками свет может быть по-разному окрашен (light color), он может затухать на определенном расстоянии (attenuation), а также порождать тени от объектов (shadows). К сожалению, большинство 3D-программ (и "стандартный" 3D Studio MAX здесь не исключение) не моделируют корректно рассеянный свет (ambient light), что напрямую сказывается на фотореалистичности итоговой визуализации.

пересчет из полярной сферической системы

Например, пересчет из полярной сферической системы координат в картезианскую будет выглядеть так:

х = rsin0-cos p;

у = r-sin0-sir p; z = r-cos0.

Прозрачность

Значение прозрачности определяет, какая часть светового потока проходит через материал. Падающий на повехность свет рассеивается и ослабляется при прохождении через прозрачный материал тем сильнее, чем меньше значение этого параметра.

Рабочее пространство

Определение "трехмерная" в названии этой главы заставляет пристальнее взглянуть на рабочее пространство, которым оперируют соответствующие программные средства. Понятно, что традиционная 2D-плоскость рисунка (как, например, в графических редакторах CorelDRAW, Adobe Illustrator или Macromedia FreeHand) для этой цели не подходит. В данном случае потребуется такое описание рабочего пространства, в котором можно создавать не только геометрическую форму моделируемых трехмерных объектов, но и их взаимное расположение как в статике, так и в движении.

Картезианская система координат

Рис. 13.1. Картезианская система координат

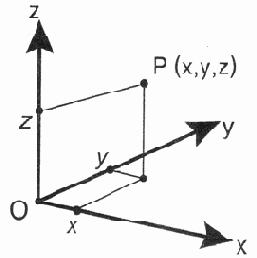
Обычно эти три оси координат (coordinate axis) обозначаются как ось х (абсцисса), ось у (ордината) и ось z (аппликата), а отложенные на них координаты точки записываются как (х, у, z).

Точка с координатами (0, 0, 0) называется началом системы координат (origin).

Также надо заметить, что существует два варианта таких прямоугольных систем координат: правосторонняя и левосторонняя. Чтобы разобраться в них, достаточно нарисовать на листе бумаги ось х горизонтально (положительные значения отложены справа от начала координат), а ось у вертикально (положительные значения сверху от начала координат). Теперь, если на оси z, проведенной перпендикулярно плоскости листа, положительные значения идут от листа к зрителю, то это правосторонняя система координат. В противном случае система координат — левосторонняя.

Реже, но все же достаточно часто, используются две другие системы координат: полярная цилиндрическая система координат (polar cylindrical coordinate system) и полярная сферическая система координат (polar spherical coordinate system).

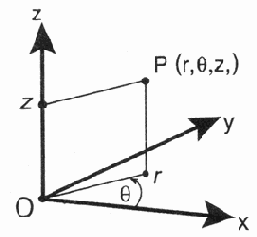
В цилиндрической системе координат (рис. 13.2) положение точки в пространстве также описывается тремя координатами (r, 0, z):

r— это расстояние от начала координат (точки 0) до проекции точки Р на плоскость ху;
0 — это угол между фиксированной плоскостью xz и полуплоскостью, проходящей через точку Р и ось z,
z — расстояние от точки Р до плоскости ху.

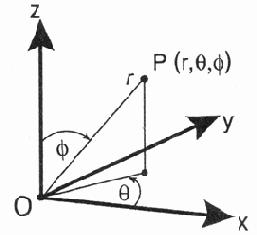
В сферической системе координат (рис. 13.3) положение точки в пространстве задается тремя координатами (r, 0, р):

r — расстояние от начала координат;
углом 0 (азимут) между фиксированной плоскостью xz и полуплоскостью, проходящей через точку Р и ось z,
углом р (зенит) между фиксированной полярной полуосью Oz и лучом, проведенным через начало координат (точку 0) и точку Р.

Цилиндрическая система координат

Рис. 13.2. Цилиндрическая система координат

Сферическая система координат

Рис. 13.3. Сферическая система координат

Отметим, что координаты точки могут быть взаимнооднозначно пересчитаны из одной системы координат в другую.

Онлайновые кривые

Рис. 13.4. Онлайновые кривые

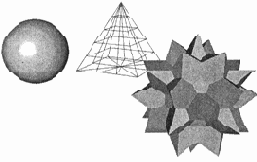
Полигональные объекты (polygonal objects) (рис. 13.5) — это полигональные примитивы (polygonal primitives), описываемые наборами динамически изменяемых параметров (например, длин, радиусов) или полигональные сетки (polygonal meshes), определяемые как наборы граней (faces), ограниченных ребрами (edges), попарно соединяющими вершины (vertices). Использование примитивов резко облегчает дизайнеру (и программе!) манипулирование формой объекта, однако служит определенным ограничением при построении сложных полигональных поверхностей. При визуализации таких ЗD-примитивов (например, сфер или ЦИЛИНДРОВ) ИХ форма аппроксимируется гранями с заданной точностью (речь идет о так называемой "сегментации"). Так как поверхность полигонального объекта представляет собой, в конечном счете, набор плоских граней, то для придания ей визуальной гладкости применяют различные алгоритмы сглаживания (smoothing). В виду относительно малой затратности вычислительных ресурсов компьютера при интерактивной визуализации таких объектов данная технология моделирования широко используется при создании 3D-игр и виртуальных миров.

Полигональные объекты

Рис. 13.5. Полигональные объекты

Поверхности Безье (Bezier patches) (рис. 13.6) — это математически гладкие поверхности, описываемые расположением вершин Безье. Эти вершины определяют их кривизну при помощи дополнительных управляющих точек (control points) на концах касательных к поверхности векторов (tangent vectors). Подобные поверхности требуют большей нагрузки для вычислительной системы, зато позволяют моделировать сложные криволинейные (например, даже органические) формы объектов.

NURBS-поверхности (Non-Uniform Rational B-splines surfaces) (рис. 13.7) — это наиболее универсальный и эффективный способ моделирования неоднородных криволинейных поверхностей. Такие поверхности описываются в особом четырехмерном гомогенном (однородном) пространстве (homogeneous space), в котором каждая управляющая вершина (control vertex), кроме трех координат х, у и z, имеет еще и дополнительную весовую (weight) характеристику. Изменяя положение и относительный вес вершины, можно предельно точно управлять формой объекта.

Составные объекты (compaund objects) (рис. 13.8) представляют собой комбинацию (или если угодно, композицию) двух или более смоделированных заранее заготовок. В зависимости от того, какое именно составное тело создается, заготовками могут служить кривые или объемы (поверхности). Типичными примерами составных объектов служат: лофт-объекты (loft objects) — тела, построенные по сплайновым сечениям; булевы объекты (boolean objects) - результаты булевских операций (объединения, вычитания или пересечения) между объемами; морфобъекты (morph objects) — анимационные объекты, изменяющие свою форму за счет интерполяции положения вершин поверхности между базовым (base) и целевыми (target) объектами.

Поверхность Безье

Рис. 13.6. Поверхность Безье

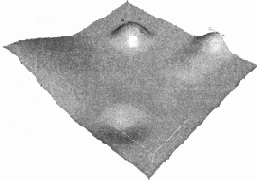
NURBS-поверхность

Рис. 13.7. NURBS-поверхность

Системы частиц (particle systems) (рис. 13.9) - это объекты-эмиттеры (emitters), генерирующие по заданному алгоритму частицы с определенной формой, начальной СКОРОСТЬЮ, СРОКОМ "ЖИЗНИ" И другими характеристиками. Такие анимационные объекты используются для моделирования дождя, пузырьков газа в жидкости, осколков взрывающихся снарядов и тому подобных образцов объективной реальности.

Составной объект и его элементы

Рис. 13.8. Составной объект и его элементы

Система частиц

Рис. 13.9. Система частиц

Динамические объекты

Рис. 13.10. Динамические объекты

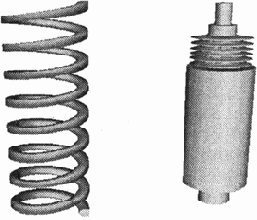Динамические объекты (dynamics objects) (рис. 13.10) позволяют моделировать объекты, реагирующие на приложенные к ним внешние силы: пружины (springs) и амортизаторы (dampers). Используются при моделировании динамики движения объектов, когда пружина, например, сама растягивается под воздействием подвешенного на ней груза.

В других программах трехмерного моделирования предоставляется во многом схожий, а в чем-то и отличный, набор инструментов создания и редактирования геометрических объектов.

Пример организации освещения

Рис. 13.11. Пример организации освещения

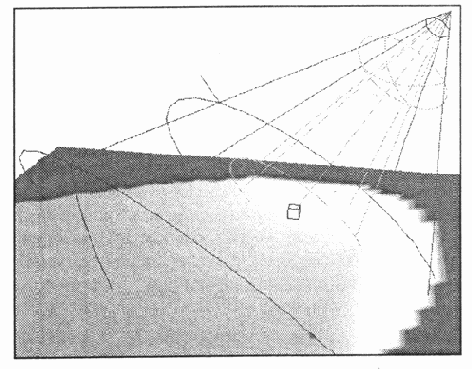
Информацию об итоговой визуализации см. в разд. "Визуализация" данной главы.

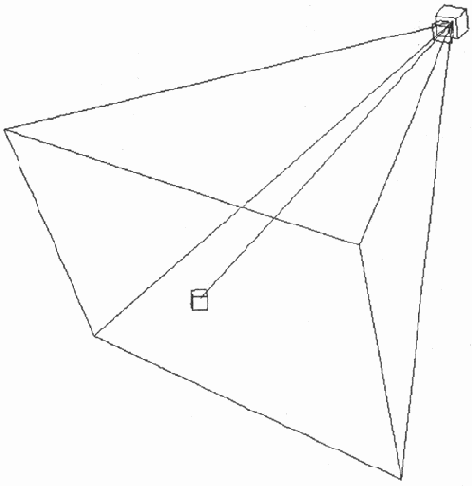
Камеры (cameras) позволяют полностью контролировать отображение объектов в плоскости кадра (рис. 13.12). Важнейшей характеристикой является фокусное расстояние объектива камеры (focal length), определяющее ее поле зрения (field of view — FOV). Оба этих параметра взаимосвязаны и измеряются в миллиметрах и градусах соответственно. Еще одной важной характеристикой камеры являются плоскости отсечения (clipping planes), ограничивающие видимую по глубине (расстоянию от наблюдателя) часть сцены (фотографы определяют этот параметр как "глубину резкости").

Пример установки камеры

Рис. 13.12. Пример установки камеры

Системы сочленений (bones systems) (рис. 13.13) — это структуры, состоящие из иерархически связанных "костей", описывающих сложную кинематику движения (kinematics) моделируемого объекта (например, человека). Обычно они применяются при использовании инверсной кинематики (inverse kinematics — IK) как метода манипулирования связанными структурами объектов. Оставаясь невидимыми при визуализации, они являются своеобразной арматурой (скелетом) анимируемого объекта или нескольких объектов.
Искривители пространства (space warps) (рис. 13.14) реализуют динамические воздействия внешних сил на объекты, это — своеобразные силовые поля, влияющие на определенные объекты. Примерами могут служить волновая деформация поверхности (wave) или ударная волна (pbomb), разбрасывающая фрагменты объекта в пространстве.

Пример сочленений

Рис. 13.13. Пример сочленений

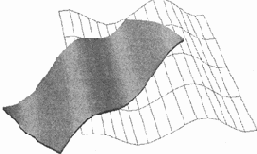
Рис. 13.14. Искривитель пространства

UV-координатный способ проецирования текстур

Рис. 13.15. UV-координатный способ проецирования текстур

UV-координатный (object UV) (рис. 13.15) — использует задаваемые в вершинах объекта параметрические координаты текстурирования поверхности. Применяется при текстурировании объектов со сложной топологией. Возможны следующие режимы отображения текстуры:
черепичный (tile) — многократным повторением текстуры по поверхности;
зеркальный (flip) — с реверсивным переворотом текстуры при ее повторении;
с усечением (clip) — "этикеточный" режим, при котором текстура не повторяется более одного раза на повехности;
С увеличением (expand) — перекрытие всей поверхности объекта одной копией текстуры.

Следует обратить внимание, что обеспечивается возможность независимого управления отображением текстуры в вертикальном и горизонтальном направлениях. Например, достаточно легко смоделировать цоколь стены повторением нужной текстуры только по горизонтали.

Системы координат

Все программы ЗD-графики, прежде всего, позволяют использовать декартову (картезианскую) систему координат (Cartesian coordinate system) (рис. 13.1), которую мы уже упоминали выше.

Более подробно о декартовой системе координат см. в части III.

В этой системе координат положение произвольной точки Р в пространстве задается тремя вещественными числами (координатами), обозначающими перпендикулярные проекции этой точки на три фиксированные, взаимоперпендикулярные, градуированные линии, называемые осями координат.

Специфика трехмерной графики

Наряду с программами традиционной 2D-графики в последнее десятилетие широчайшее распространение и популярность получили программы 3D-моделирования, анимации и визуализации. При этом такие известные программные решения, как 3D Studio MAX от компании Discreet (подразделения Autodesk, Inc.) или Maya от компании Alias | Wavefront являются, по сути, гибридными графическими пакетами. С одной стороны, они предоставляют дизайнеру возможность манипулирования 2D- и 3D-векторными объектами, с другой, результатом работы (финальной визуализации) является пиксельное (растровое) изображение — отдельный кадр или видеоролик.

В силу специфики 3D-моделирования и возможности работать с анимацией (отображение изображений во временном развитии) такие программы занимают особое место в линейке графических программ. Если попытаться позиционировать пакеты 3D-графики с точки зрения их целевой функции, можно выделить следующие занимаемые ими сегменты1 рынка.

Визуальные спецэффекты для кино- и видеоиндустрии. Телевизионная реклама. Интерактивные игры.
Промышленный и архитектурный дизайн.
Научная, медицинская и судебная визуализация.
Компьютерные тренажеры и обучающие программы.

Завершая этот краткий обзор, следует отметить, что использование пакетов трехмерной графики предъявляет повышенные требования как к аппаратно-программным средствам используемого компьютера, так и к уровню знаний работающего с ними дизайнера.

Текстурирование материалов

Использование текстурных карт (декоративных узоров, maps) позволяет придать материалам дополнительную реалистичность (например, вид мощенной плиткой мостовой или портмоне из крокодиловой кожи).

В качестве карт могут быть использованы изображения (image textures), сохраненные в файлах различных форматов (BMP, TIF, JPG, EPS и некоторых других), либо процедурные текстуры (procedural textures), являющиеся наборами правил (процедурами) быстрого построения нужного узора.

Типичным примером применения карт при моделировании материалов является описание их с помощью текстурирования цвета поверхности или ее рельефа (bump mapping).

Типы пространств

В зависимости от задачи и этапа работы (например, исходное моделирование формы объекта или последующее размещение уже готовых объектов на "сцене") можно выбирать различные типы пространств и связанных с ними координатных систем.

Чаще всего программы трехмерного моделирования предоставляют следующие варианты пространств.

Пространство объекта (object space), которое предназначено для моделирования (описания) формы объекта в его собственной (локальной) системе координат безотносительно того, где он будет размещен на сцене, как ориентирован или масштабирован. У каждого объекта существует своя собственная система координат.
Мировое пространство (world space) используется для размещения объектов на сцене, осуществления аффинных трансформаций (перемещения, поворота и масштабирования объектов), описания освещения сцены, вычисления столкновений между объектами при моделировании динамики их движения и т. п. Это единое пространство для всех объектов.
Видовое пространство (view space) ассоциировано с виртуальным наблюдателем (обычно камерой) или определенной проекцией сцены (например, фронтальным видом) и описывает ту часть сцены, которая доступна для просмотра и работы в видовом окне (viewport). Это — своего рода точка зрения.
Экранное пространство (screen space) — это D-пространство (плоскость), в котором отображаются аксонометрические (axonometric) или перспективные (perspective) проекции ЗВ-объектов на плоскость поверхности монитора.
UVW-параметрическое пространство (UVW parametric space) используется при математическом моделировании сложных кривых и поверхностей (например, NURBS-объектов) или для задания UVW-координат тексту-рирования поверхностей (UVW mapping coordinates).

Более подробную информацию о параметрическом представлении кривых см. в главе 12 данной части.

Управление текстурированием

Для точного управления текстурированием (texture alignment) обычно требуется дополнительно указать способ проецирования ("переноса") текстуры на поверхность объекта (projection type) и режим отображения на ней (mapping mode).

Основные способы проецирования текстур следующие:

ортографический (orthographic)— когда текстура проецируется на плоскость, описанную тремя точками. Такой способ очень часто называют планарным (planar) проецированием;
цилиндрический (cylindrical) — это "заворачивание" объекта в текстуру, проецируемую на цилиндр, описанный двумя полюсами (верхним и нижним) и линией шва (соединения кромок текстуры);
сферический (spherical) — способ, аналогичный предыдущему, но проецирование происходит на сферу, заданную верхним полюсом, центром и швом;
зеркальный (reflection) — применяется для имитации отражений на поверхности объекта. Работает подобно сферическому проецированию;

Визуализация

Итоговая визуализация (rendering) — заключительный этап работы со сценой, в своем роде, момент истины.

К этому этапу сцена будет содержать информацию о геометрии объектов, их материалах и освещении. Задача модуля визуализации состоит в том, чтобы вычислить цвет каждого пиксела итогового изображения, основываясь на информации о моделях и выбранном положении виртуального наблюдателя (камеры).

Цвет каждой точки на поверхности отрисовываемого объекта вычисляется исходя из физических свойств материала и освещающего его света. Для описания того, как поверхность отражает или пропускает свет, существует два основных алгоритма тонирования (shading algorithms). Они называются алгоритмами локального (local illumination) и глобального освещения (global illumination).

Ввиду особой сложности области трехмерной

Ввиду особой сложности области трехмерной графики данная глава, написанная И. Б. Петровым, представляет собой только конспективное перечисление всех элементов.