Базовые функции

Функция, которая определяет, как сильно форма кривой зависит от конкретной контрольной точки Вi, называется базовой функцией (basis function) этой контрольной точки.

Часть IV

Часть IV

.

ВЕКТОРНАЯ ГРАФИКА

Глава 12. Принципы векторной графики Глава 13. Трехмерная графика

Данная часть так же, как и предыдущая часть III, является основной и предлагает полное описание другого способа кодирования графической информации — векторной графики. Эта часть является в книге самой трудной, поскольку целиком основана на абстрактных математических принципах.

Принципы векторной графики основаны на ином математическом аппарате и имеют целью построение линейных контуров, составленных из элементарных кривых, описываемых математическими уравнениями в особой параметрической форме.

Для того чтобы линейные контуры, составленные из элементарных кривых, не создавали резких преломлений и разрывов, элементарные кривые должны быть гладкими, что обеспечивается специальным размещением управляющих линий. Общим видом таких кривых являются NURBS-кривые, а более частным — кривые Безье. Первые и вторые используются в трехмерной графике, а вторые — только в программах плоской векторной графики.

Векторная графика в английской терминологии обозначается словами "drawing" или "illustration".

Гладкие кривые

Все умные места кривые.

Мераб Мамардашвшш

Одной из самых важных причин выбора в качестве средств векторной графики кривых Безье и NURBS-кривых является управляемая гладкость. Гладкость означает, что при моделировании на кривой не образуется петель и резких преломлений (тем более разрывов). Но при этом, не исключена возможность создания как гладкого сопряжения, так и изгибов, например острых углов.

Прекрасным примером такого сочетания гладких кривых и острых преломлений являются профили авиакрыла. Обсудим гладкость кривых.

В этой главе рассматриваются принципы

Глава 12.

Принципы векторной графики

В этой главе рассматриваются принципы векторной графики: формулы и способы построения. Данная глава написана совместно с Иваном Борисовичем Петровым.

Дискретизация (на сей раз линейная) позволяет создавать произвольные векторные контуры из элементарных кривых, построенных на основе какой-либо единой формулы.

Отсюда формулируется задача — поиск формулы, которая бы позволяла описывать все многообразие линейных контуров. И поскольку дискретизация имеет линейный характер, общий контур разбивается на достаточно мелкие фрагменты — сплайны. При этом необходимо выбрать наиболее простую формулу (функцию) для их описания, представляемую в параметрической форме. Одной из самых важных причин выбора в качестве средств векторной графики кривых Безье и NURBS-кривых является управляемая гладкость, а также то, что их форма определяется расположением множества контрольных точек, которые определяют форму только части кривой, находящейся рядом.

В программах векторной графики единственный способ изменения формы — интерактивное перемещение опорных и управляющих точек. На базе кривой Безье основывается и язык описания страниц PostScript, развитие которого шло по пути интегрирования новых возможностей выводных устройств (цветной печати, систем управления цветом и шрифта).

Принципы векторной графики

ЧАСТЬ IV ВЕКТОРНАЯ ГРАФИКА Глава 12 Принципы векторной графики Общие принципы векторной графики Исторические предшественники Параметрические уравнения Гладкие кривые NURBS-кривая Контрольные точки Базовые функции Узлы Характеристика семейства базовых функций Рациональные кривые Кривая Безье (формулы и принципы построения) Свойства кривых Безье Канонический вид кривой Безье Изменение формы кривой Соединение нескольких секторов Типы опорных точек Язык PostScript Краткая информация о векторных форматах файлов Векторный формат WMF Векторный формат EPS Векторный формат PDF Векторный формат AI Векторный формат CDR Векторный формат FH

Характеристика семейства базовых функций

Для любого значения параметра t сумма всех базовых функций строго равна 1.

Если веса всех контрольных точек положительны, кривая лежит в области, полученной соединением крайних (внешних) контрольных точек. Такой "габаритный" контейнер получил название "выпуклой оболочки" (convex hull).

Исторические предшественники

Учение о природе будет содержать науку в собственном смысле лишь в той мере, в какой может быть применена в нем математика.

Иммануил Кант

В докомпьютерные времена специалисты, которые работали с линейными изображениями (архитекторы, кораблестроители и инженеры) для создания своих проектов пользовались только бумагой, карандашами и простейшими чертежными инструментами (линейками, циркулями, угольниками и транспортирами). Однако при создании чертежей больших деталей в натуральную величину, например шпангоутов судов, возникали естественные сложности. Причем проблема состояла не только в размере, но скорее в том, чтобы провести гладкую кривую через определенное количество заранее фиксированных точек.

Пытливая мысль и изобретательность нашли оригинальный способ: в больших помещениях нужную форму кривой получали, выгибая длинные тонкие полоски дерева или металла. Такие полоски называли сплайнами (splines). Для того чтобы придать упругой полоске нужную форму, ее фиксировали в требуемых точках с помощью особых свинцовых грузил, которые за сходство формы назывались "утятами" (ducks). Результирующая кривая получатась гладкой, а форма изменялась перемещением грузил (рис. 12.1).

Изменение формы кривой

Как же изменить форму канонической кривой Безье, чтобы с ее помощью получить огромное многообразие форм, из которых можно составить объект любой бложности?

В программах векторной графики существует единственный способ — это интерактивное перемещение опорных и управляющих точек. Если перемещаются начальная или конечная точки, то кривая станет соответствующим образом изменяться (вытягиваться или сжиматься как упругая резинка). Перемещение управляющих точек изменяет кривизну соответствующей "половинки" кривой Безье, входящей в начальную или конечную точки (рис. 12.28).

Канонический вид кривой Безье

Рассмотрим канонический вид кривой Безье и попытаемся понять, как из одной-единственной кривой получается бесконечно большое многообразие форм, которые используются в векторной компьютерной графике.

Общий вид кривой Безье имеет вот такую конструкцию (рис. 12.25).

Контрольные точки

Для начала следует вспомнить определение параметрической кривой, которое упоминалось ранее.

Определение параметрических функций см. в разд. "Параметрические уравнения" данной главы.

В этом определении левая часть выражения, описывающая функцию q, выглядит так:

q(t) = ...,

где t — параметр, представляющий заданный набор значений определенного диапазона, как правило, от 0 до 1. Используя эти значения, получают последовательность пар {х, у}, по которым строится моделируемая кривая (рис. 12.6).

Краткая информация

Краткая информация

о векторных форматах файлов

Векторный формат WMF

Векторный формат WMF (Windows Metafile) применяется для хранения векторных изображений, например в этот формат конвертируются векторные изображения при переносе через буфер обмена Clipboard, поэтому для редактирования данного формата никакого специального приложения не существует.

Кривая Безье (формулы и принципы построения)

В общем случае кривая Безье — это частный случай В-СПЛЗЙНОВ (NURBS-кривых), которые можно определить как взвешенная сумма п+ 1 контрольных точек, где весовыми коэффициентами являются полиномы Бернштейна. Рассмотрим определения первых трех степеней кривой Безье.

Линейная кривая, кривая первой степени (прямая), определяется следующей параметрической формулой:

P(t) = (1 - t)P0+tP1

Это выражение представляет собой линейную интерполяцию между двумя точками (рис. 12.17).

NURBS-кривая

Обсуждение стоит начать с объяснения термина NURBS, который является аббревиатурой (сокращением) и расшифровывается как Non-Uniform Rational B-spline, где:

"Non-Uniform" (неоднородный) означает, что область влияния контрольной точки на форму кривой может быть различной. Это очень важное свойство для моделирования иррегулярных кривых.
"Rational" (рациональный) означает, что математическое выражение, описывающее форму моделируемой кривой, есть отношение двух полиномов.

Эта особенность позволяет точнее моделировать различные кривые, например конические сечения.

"B-spline" (basis spline, базовый сплайн) — способ математического описания кривой интерполяцией между тремя и более контрольными точками.

Общие принципы векторной графики

Разум так же близок к истине, как многоугольник к кругу, ибо чем больше число углов вписанного многоугольника, тем больше он приблизится к кругу, но никогда не станет равным кругу даже и в том случае, когда углы будут умножены до бесконечности.

Николай Кузанский

Из школьного курса, который вы, может быть, успели забыть, следует, что определенную линию, например прямую или параболу, можно представить двумя способами:

аналитически, когда используется математическая формула; графически, или геометрически, когда она изображается визуально на плоскости.

Соблазнительно предположить, что и все многообразие линейной графики можно представить в виде формул, которые бы ее описывали и позволяли экономно фиксировать.

Замечание

Вспомним кстати, что пиксельная графика, которая рассматривалась в части III, по критерию экономичности явно проигрывает линейной графике.

Но дело осложняется тем, что составление такой формулы является отнюдь не тривиальной задачей и ее создание может потребовать такое огромное количество времени, что эта процедура станет абсолютно нерентабельной. Более того, необходимость непрерывно изменять форму кривой полностью делает еще более затруднительным такое предположение. Но и расставаться с такой возможностью жаль.

Поэтому, естественно, в этой ситуации возникает идея, как бы с помощью одной-единственной формулы описать все многообразие кривых, используемых в линейной графике.

Но как это сделать? Следует опять мысленно вернуться к принципам пиксельной графики, в основе которой лежит технология дискретизации (разделение плоского изображения на равные площадки — пикселы) и попытаться применить тот же принцип для линейных изображений.

Информацию о принципах пиксельной графики см. в части III.

Разумеется, теперь и дискретизация приобретет иной характер — линейный, т. е. пространственная дискретизация, на которой основана пиксельная графика, сменится на линейную, поскольку имеется только одно измерение — вдоль линии.

И если уж разбивать произвольные кривые на отдельные фрагменты (сегменты), разумно принять следующие исходные условия:

разбивать линии на достаточно мелкие (короткие) фрагменты; выбрать наиболее простую формулу (функцию) для их описания.

Самой простой функцией, естественно, является линейная зависимость, с помощью которой описывается прямая линия — кратчайшее расстояние между двумя точками, лежащими на плоскости.

Разбивая линейный рисунок на достаточно мелкие элементы дискретизации и соединяя полученные точки дискретизации прямыми, можно с помощью исчислимого (конечного) количества этих прямых представить любой линейный объект и любую сложную кривую.

Самым главным достоинством такой технологии является, естественно, простота; для каждой точки достаточно всего двух чисел, определяющих координаты этих точек. Таким образом, огромную кривую можно описать всего-навсего сотней пар чисел.

Однако указанная простота является причиной серьезных недостатков.

Объекты, составленные только из прямолинейных сегментов, лишаются возможности произвольного масштабирования. Пока отрезки достаточно мелкие, они не создают впечатления угловатости, но при значительном коэффициенте увеличения углы становятся очевидными.
Форма объекта, аппроксимированного линейными отрезками, может изменяться, например при вращении.
Для совершенно достоверной аппроксимации формы объекта, когда окружность выглядит как окружность, а не как многоугольник, потребуются десятки тысяч линейных сегментов.

Содержание главы

Параметрические уравнения

Как уже было сказано выше, кривые можно представлять аналитически и графически, т. е. как график функции. Математики записывают это следующим образом:

что означает "значение у — это функция, т. е. зависимость, от значения х", например простейшая функция у = 2х означает простейшую зависимость: каждое значение у в два раза больше любого значения х. График этой функции представляет собой прямую линию, проходящую через начало координат (рис. 12.2).

Более интересный вид представляют собой тригонометрические функции, например синусоида:

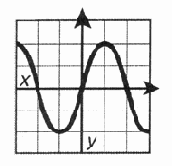
у = sin х. График такой кривой известен каждому (рис. 12.3).

Пример-метафора

Упрощенно говоря, задача формулируется так: найти некий набор заготовок, каких-нибудь бесконечно гибких проволочек, из которых мы единообразным способом с помощью одной и той же формулы получим самые разные формы.

А уже из этих форм составим цепочку, т. е. последовательно свяжем их друг с другом и получим любой произвольный объект.

Для того чтобы перейти к таким кривым, необходимо вспомнить об исторических корнях.

Пример-метафора

Можно легко представить, что значения параметра t— это отсчеты времени, в течение которого происходит перемещение определенной частицы вдоль произвольной кривой, например окружности. Параметрическая функция q(t) позволит получать пары координат {х, у}, по которым перемещается частица в различные моменты (значения) времени f. Хотя, в общем случае, не обязательно параметр t связывать со временем.

Вторым важным качеством параметрических кривых является то, что они имеют более разнообразные формы, чем это позволяют явные уравнения.

Пример-метафора

Продолжая метафору частицы, перемещающейся по кривой, можно сказать, что у нее на пути вдоль параметрической кривой не должно быть остановок (кроме начала и конца) и внезапного изменения направления.

Для того чтобы представить направление движения частицы, можно мысленно "укрепить" на ней стрелку, которая непрерывно указывает направление движения вдоль параметрической кривой.

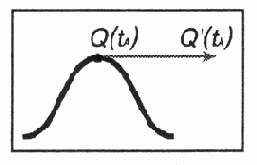
На математическом языке стрелка на частице называется касательной. Если касательная в соседних точках не меняет внезапно своего направления, такую кривую считают гладкой (рис. 12.4).

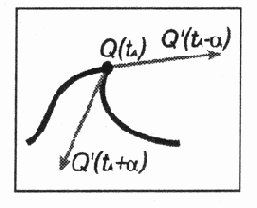
Если «на кривой имеется излом, то направление касательной в точке Q меняется практически мгновенно (рис. 12.5).

Пример-метафора

В каждый данный момент положение движущейся частицы определяется как весовое усреднение положения всех контрольных точек. При этом контрольные точки, расположенные ближе к частице, оказывают большее влияние (как, например, большая масса небесного тела притягивает сильнее, поскольку сила гравитации у такого тела больше) при определении ее итогового положения в пространстве. Другими словами, для определения положения движущейся частицы необходимо просуммировать положение всех контрольных вершин (точек) с учетом меняющейся "значимости" (гравитации).

Если кому не очень ясен пример с гравитацией, можно предложить другую метафору. Выбор и покупка, скажем, холодольника определяются многими факторами (ценой, объемом, цветом и т. п.). Но эти факторы не равнозначны, каждый фактор имеет свою значимость, например цена важнее цвета, это значит, что у цены больший "вес" в сравнении с цветом. Если просуммировать "веса" всех факторов, то можно формально "вычислить", какой холодильник разумнее приобрести.

Пример-метафора

Можно описать значения функции для выбранного значения параметра t, например, таким образом: 30% положения одной контрольной точки плюс 60% — другой и плюс 10% — третьей. Это, в частности, означает, что когда движущаяся частица удаляется от некоторой контрольной точки, она испытывает все меньшее воздействие. И наоборот, при приближении частицы к контрольной точке ее положение все больше от нее зависит. И такой эффект повторяется всякий раз, когда движущаяся частица проходит все контрольные точки.

Теперь следует сосредоточиться как раз на том, что подобное "влияние" контрольной точки может быть не только выражено числовыми значениями, но и визуализировано на графике (коль скоро это тоже функция). Таким образом, можно построить график базовой функции как зависимость влияния на движущуюся частицу, например в процентах, от значения 1(рис. 12.9).

Максимальный эффект (максимальное влияние) достигается в совершенно определенной точке и постепенно уменьшается по мере удаления. Форма кривой, описывающей эту зависимость, напоминает колокол.

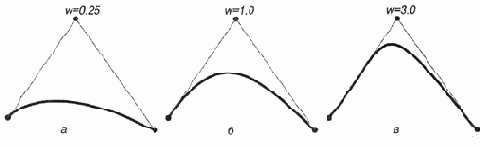
кривая определяется тремя контрольными точками

Квадратичная (второй степени) NURBS- кривая определяется тремя контрольными точками (рис. 12.16). У всех трех кривых узловой вектор имеет вид {0.0, 0.0, 0.0, 1.0, 1.0, 1.0}. Веса первой и последней контрольных точек у каждой кривой равны 1. Если вес центральной вершины меньше 1, то результирующая кривая представляет собой сегмент эллипса (рис. 12.16, а). Если ее вес равняется 1, образуется парабола (рис. 12.16, б). Если же ее вес гораздо больше 1, то кривая преобразуется в гиперболу (рис. 12.16, в).

в явном виде не позволяют

Графики синусоиды и косинусоиды в явном виде не позволяют замкнуть линию, а две параметрические функции

x(f) = cost;

y(t) = sinf

создают окружность, если t "пробегает" значения между 0 и 360 градусов.

Рациональные кривые

Обратимся к ключевой букве в названии NURBS — "R", что означает "rational" (рациональный). Рациональные кривые, в сравнении с обычными (нерациональными — "non-rational") В-сплайнами, обладают двумя дополнительными и очень важными свойствами:

они обеспечивают корректный результат при проекционных трансформациях (например, масштабировании), а нерациональные В-сплайны — только при аффинных трансформациях (например, перемещениях);
их можно использовать для моделирования кривых любого вида, включая конические сечения (окружности, эллипсы, параболы и гиперболы).

Эти свойства (кстати, весьма значительные) достигаются за счет четырехмерного представления обычной трехмерной контрольной точки {х, у, z}. Это значит, что каждая контрольная точка представляется четырьмя координатами {х, у, z, w}. Последняя координата w означает вес (weight) контрольной точки, о котором уже упоминалось ранее (вспомним пример с гравитацией или холодильником).

Чертежные сплайны

Рис. 12.1. Чертежные сплайны

Впоследствии понятие сплайна стали применять в математике для похожей цели — описания кривых.

В 1885 году Карл Вейерштрасс сформулировал и доказал теорему, названную его именем. Примерно в таком виде она приводится в современных курсах математического анализа: в соответствии с этой теоремой для любой непрерывной на отрезке функции найдется многочлен, сколь угодно мало отличающийся от данной функции. В более простой формулировке это означает, что согласно доказанной теореме Вейерштрасса можно обрисовать любую функцию с помощью полиномов.

График функции у = 2х

Рис. 12.2. График функции у = 2х

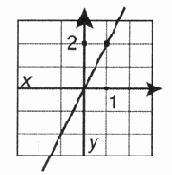
График функции у = sinx

Рис. 12.3. График функции у = sinx

Такой способ представления формулы и ее графика называется явным. Он позволяет относительно легко строить график. Однако у этого способа с точки зрения графического представления имеются весьма существенные недостатки.

Каждому значению х соответствует только одно значение у. Это не дает возможности начинать новый фрагмент кривой в произвольном месте.
Кривая не может быть замкнутой.

В результате явный способ представления не может применяться там, где требуется описание произвольных кривых, размещаемых в произвольных местах на плоскости.

Альтернативным способом является определение кривой как параметрической функции.

В первую очередь очень важно отметить следующую особенность: у такого способа обе координаты (х и у) являются равноправными, т. е. вычисляются как функции некоего вспомогательного параметра, обозначаемого, как правило, символом t. В общем случае такая зависимость получает вид:

q(t) = {x(t), y(t)},

где х(t) и y(f) — функции параметра t.

Задавая одинаковые значения t, функция x(f) вычисляет значения координаты х, а функция y(t) — значения координаты у.

Касательная на гладкой кривой

Рис. 12.4. Касательная на гладкой кривой

Касательная на кривой с изломом

Рис. 12.5. Касательная на кривой с изломом

Теперь мы должны подробнее познакомиться с основами построения гладких кривых, применяющихся в векторной компьютерной графике. Начнем с NURBS-кривых, которые являются более общим (а соответственно, и более сложным) случаем таких кривых.

Пример построения параметрической кривой

Рис. 12.6. Пример построения параметрической кривой

В указанном выше выражении не определена правая часть, т. е. собственно параметрическое уравнение, а точнее, параметрические уравнения.

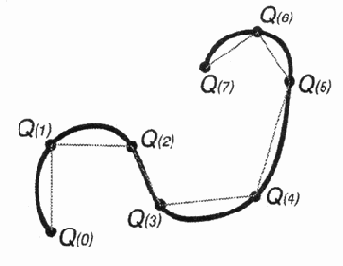
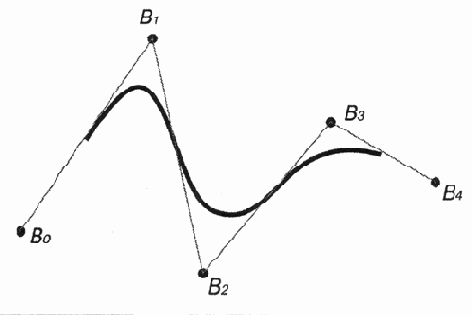
Одной из основополагающих особенностей NURBS-кривой является то, что ее форма определяется расположением множества контрольных точек (control points). На рис. 12.7 эти точки обозначены как Bi.

Множество контрольных точек, определяющих параметрическую кривую

Рис. 12.7. Множество контрольных точек, определяющих параметрическую кривую

Эта особенность NURBS-кривой важна, поскольку позволяет локализовать изменение формы кривой перемещением отдельных контрольных точек без изменения формы всей кривой в целом (рис. 12.8).

Изменение формы фрагмента кривой, вызванное перемещением контрольной точки

Рис. 12.8. Изменение формы фрагмента кривой, вызванное перемещением контрольной точки

Каждая контрольная точка определяет форму только той части кривой, которая находится в ее окрестности, и оказывает меньшее воздействие или вовсе не влияет на форму оставшейся части кривой.

Типичный график базовой функции отдельной контрольной точки

Рис. 12.9. Типичный график базовой функции отдельной контрольной точки

Поскольку каждая контрольная точка "обязана" иметь свою базовую функцию, NURBS-кривая, построенная, например, по пяти контрольным точкам, должна иметь пять таких функций, перекрывающих некоторую область результирующей кривой (рис. 12.10).

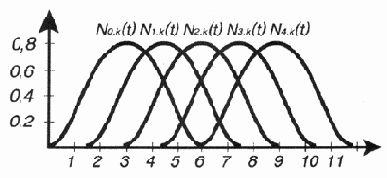
Рис. 12.10. Однородные базовые функции для множества контрольных точек

Пример однородного узлового вектора

Рис. 12.11. Пример однородного узлового вектора

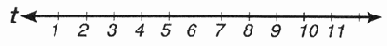
Следующий рисунок (рис. 12.12) представляет пример кривой, созданной на основе такого узлового вектора.

NURBS-кривая с однородным узловым вектором

Рис. 12.12. NURBS-кривая с однородным узловым вектором

Если изменить узловой вектор, например, следующим образом: {0.0, 1.0, 2.0, 3.75, 4.0, 4.25, 6.0, 7.0},

то получится другое множество неоднородных (non-uniform) базовых функций (рис. 12.13) и, соответственно, другая форма кривой (рис. 12.14), которая строится на тех же контрольных точках, что и на рис. 12.12.

Неоднородные базовые функции для множества контрольных точек

h2>Рис. 12.14. NURBS-кривая с неоднородным узловым вектором

Изменение формы кривой при изменении веса контрольной точки

Рис. 12.15. Изменение формы кривой при изменении веса контрольной точки

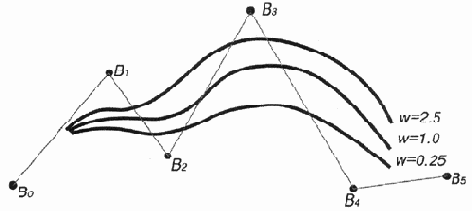
Замечание

Важно заметить, что существенным является только относительное изменение весов контрольных точек. Если вдвое увеличить веса всех контрольных точек, то форма кривой не изменится.

NURBS-кривые с различными весами центральной контрольной точки

Рис. 12.16. NURBS-кривые с различными весами центральной контрольной точки

При всех своих непревзойденных свойствах NURBS-кривые все же обладают следующим громадным недостатком: расширенные возможности не могли не сказаться на уровне и сложности инструментария для их построения, а это, в свою очередь, требует от дизайнера повышенных условий для освоения, не говоря уже о необходимости определенного уровня математической подготовки (иначе трудно ожидать, что удастся разобраться во всех преимуществах и получить творческую свободу).

Кривая первой степени (прямая)

Рис. 12.17. Кривая первой степени (прямая)

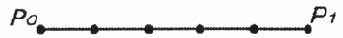
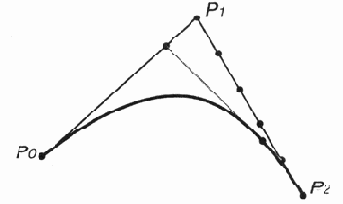
Квадратичная кривая, кривая второй степени, определяется формулой:

= (1 - t)2P0 + 2(1 - t)tP1 + t2P2.

Это выражение представляет собой линейную интерполяцию между линейными интерполяциями между точками (рис. 12.18):

Кривая второй степени (квадратическая кривая)

Рис. 12.18. Кривая второй степени (квадратическая кривая)

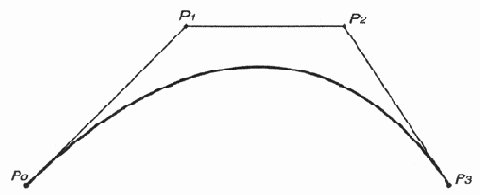
Кубическая кривая, кривая третьей степени, определяется формулой: P(t) = (1 - t)3Р0 + 3(1 - t)2tP1 + 3(1 - t)t2P2 + t3Р3.

Это выражение представляет собой линейную интерполяцию между линейными интерполяциями между линейными интерполяциями между точками (рис. 12.19).

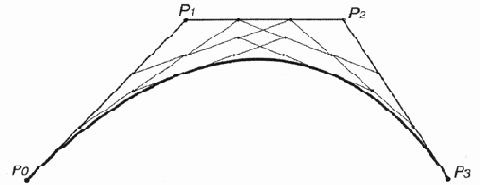
Рис. 12.19. Кривая третьей степени (кубическая кривая)

Кривая в выпуклом многоугольнике

Рис. 12.20. Кривая в выпуклом многоугольнике

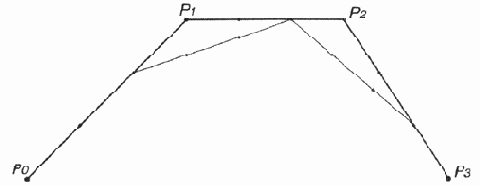
Кривую Безье можно рассматривать как пошаговое уточнение формы многоугольника, получаемого последовательным соединением ее контрольных точек (рис. 12.21—12.24). При этом кривая Безье начинается и заканчивается в конечных точках данного многоугольника, а форма определяется относительным расположением оставшихся точек, через которые в общем случае она не проходит.

Исходя из этого можно представить канонический вид кривой Безье, который обычно используется в графических редакторах плоской графики.

Первый этап аппроксимации кривой

Рис. 12.21. Первый этап аппроксимации кривой

Второй этап аппроксимации кривой

Рис. 12.22. Второй этап аппроксимации кривой

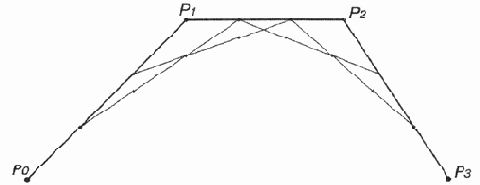
Третий этап аппроксимации кривой

Рис. 12.23. Третий этап аппроксимации кривой

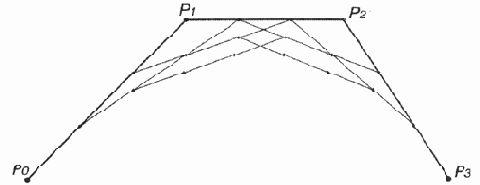
Рис. 12.24. Итоговая ломаная кривая

Канонический вид кривой Безье

Рис. 12.25. Канонический вид кривой Безье

Причем, это уже не математическое описание, а сугубо прикладное отображение, именно то, которое знакомо всем пользователям векторных программ.

Составной контур с разнонаправленными векторами

Рис. 12.26. Составной контур с разнонаправленными векторами

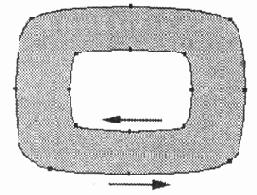
Рис. 12.27. Составной контур с однонаправленными векторами

Способы изменения формы сегмента

Рис. 12.28. Способы изменения формы сегмента

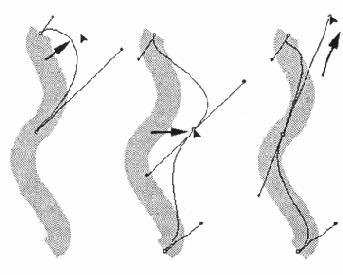
Таким образом, с помощью перемещения этих четырех точек получают неограниченное количество форм кривой Безье, которая может быть всего-навсего одним отдельным сегментом сложного секторного контура.

Разумеется, векторные редакторы позволяют работать одновременно с несколькими опорными точками (перемещать, вращать и т. п.).

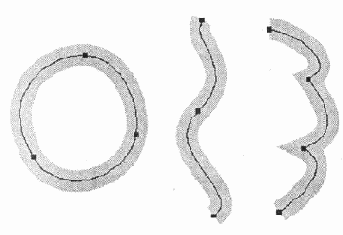
Примеры векторных контуров, составленных из кривых Безье

Рис. 12.29. Примеры векторных контуров, составленных из кривых Безье

В каждом сегменте можно добавлять опорные точки, в данном случае появляются две дополнительные управляющие точки с управляющими линиями, которые тоже позволяют изменять форму кривой. Добавление новых опорных точек в пределах одного сегмента кривой не противоречит тому условию, что отдельные кривые соединяются в цепь. Просто кривая Безье добавляется не к концу контура, а размещается внутри уже имеющегося контура.

Пример точки перегиба

Рис. 12.30. Пример точки перегиба

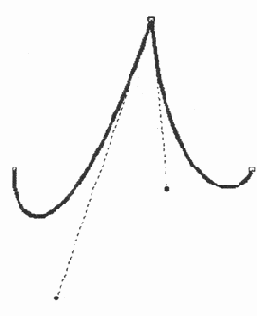
Пример гладкой точки

Рис. 12.31. Пример гладкой точки

У программы CorelDRAW предусмотрен подвид гладкого сочленения, который называется симметричный узел (symm от слова "symmetrical") (рис. 12.32). Суть его состоит в том, что управляющие линии фиксируют не только по направлению, но и по величине (длина направляющих всегда одинакова). Если одну из них увеличивать или уменьшать, другая будет синхронно повторять это действие.

Симметричная опорная точка

Рис. 12.32. Симметричная опорная точка

Пример тангенциальной точки в программе FreeHand

Рис. 12.33. Пример тангенциальной точки в программе FreeHand

Типы опорных точек можно суммировать в виде следующей таблицы (табл. 12.1).

Таблица 12.1. Типы опорных точек в различных векторных программах


Тип опорной точки	Adobe Illustrator	Macromedia FreeHand	CorelDRAW
Угловая	Corner anchor point	Corner point	Cusp node
Гладкая	Smooth anchor point	Curve point	Smooth node
Тангенциальная	—	Connector point	—
Симметричная	—	—	Symm node

Типы опорных точек в трехмерной графике имеют ту же основу, но отличаются другими характеристиками (в качестве примера можно рассмотреть опорные точки в программе Autodesk 3D МАХ).

Smooth (гладкая): вершина, через которую кривая проходит "неуправляемо" гладко. Форма кривой определяется расстоянием между соседними вершинами.
Corner (угловая): вершина, в которой кривая получает излом.
Bezier (Безье): вершина Безье с управляющими рычагами, которые не равны по длине, но ориентированы строго в противоположных направлениях. Форма кривой зависит и от направления касательных, и от длины рычагов.
Bezier Corner (угловая Безье): все характеристики идентичны опорной точке Bezier, но угол между управляющими рычагами может быть произвольным, т. е. допускается излом на кривой.

Соединение нескольких секторов

Теперь необходимо рассмотреть, как создается многообразие контуров с помощью соединения нескольких канонических кривых Безье в связанную последовательность, часто даже замкнутую (рис. 12.29).

Справка

Слово "вектор" латинского происхождения: "vector" переводится как "несущий", в математике используется для обозначения отрезка определенной длины и направления. Два вектора считаются равными лишь в том случае, если у них не только одинаковы длины, но и совпадают направления (то есть они параллельны и одинаково ориентированы). При изменении направления меняется знак вектора. В естественных науках векторы изображают величины, которые имеют направление, например сила, скорость, ускорение и т. д.

Направление кривой, может быть, не всегда очевидно для пользователей векторной программы, но для самой программы оно всегда существенно. Направление контуров находит свою реализацию в так называемых составных контурах (compound paths). Если два векторных объекта, например образующих букву "о" и расположенных друг на друге, направлены в противоположные стороны (рис. 12.26), то изображение получится верное ("с дыркой посередине").

Если те же векторные контуры направлены в одну сторону, то в этом случае один контур просто перекрывает другой, не образуя прозрачной области (рис. 12.27).

Справка

Вейершрасс Карл (1815—1897) — немецкий математик, иностранный член-корреспондент (1864) и иностранный почетный член (1895) Петербургской Академии Наук. Известен своими трудами в области математического анализа, теории функций и линейной алгебры. Главным его научным достижением считается система логического обоснования математического анализа.

Справка

Слово "полином" происходит от греческого слова "poly", что означает "многочисленный", и латинского слова "nomen" — "имя", русский эквивалент этого понятия — многочлен. Полином представляет собой алгебраическую сумму конечного числа одночленов, например для одного переменного х многочлен имеет вид

y = a0xn +a1xn-1...+an,

где а — коэффициенты многочлена, п — показатели степеней (целые неотрицательные числа). В курсе средней школы нам известны многочлены первой, второй и третьей степени.

Вопрос о построении аппроксимирующего многочлена привлек многих математиков. Среди них одну из решающих ролей сыграл выдающийся ученый Сергей Натанович Бернштейн, который закончил Харьковский университет, учился в Сорбонне, а в начале XX века предложил новое доказательство теоремы Вейерштрасса с помощью теории вероятностей. В этом случае необходимый полином строится в явном виде (не параметрически). Именно данный полином и стал основой сплайновых кривых, в частности NURBS-кривых и кривых Безье.

Пример аппроксимирования кривых Безье см. в разд. "Свойства кривых Безье" данной главы.

Справка

Бернштейн Сергей Натанович (1880—1968)— математик, академик Академии Наук СССР и Академии Наук Украины. Основные труды относятся к области теории дифференциальных уравнений (условия аналитичности решений), теории функций (приближение функций многочленами), теории вероятностей (аксиоматика, предельные теоремы).

Справка

Аппроксимация происходит от латинского слова "approximo", что переводится как "приближаюсь", в математике это означает замену одних объектов, например сложных функций, другими, более простыми, которые являются более или менее близкими к исходным. Самый простой пример аппроксимации мы уже упоминали — это замена кривых линий совокупностью прямых, образующих ломаную линию, примерно совпадающую с исходной.

К сожалению, нашему великому соотечественнику не очень повезло, поскольку чаще известны имена людей, применивших открытия, чем их авторов. То же случилось с кривыми, которые известны всему миру под именем кривых Безье.

Справка

Безье (Bezier) Пьер Этьен (1910 — 1999) — французский инженер и ученый, который, поступив в 1933 году на завод Рено, с 1960-х годов начал исследования в области компьютерного моделирования, в частности, применил на практике компьютерное проектировани теортю сплайнов трехстепенных функций, разработанных именно Сергеем Натановичем Бернштейном. Пьер Безье — автор четырех книг и множества статей по этой тематике, он почетный доктор многих ведущих университетов мира.

Теперь все компьютерные художники и дизайнеры знают "кривые Безье", "инструменты Безье", а многие пользователи компьютерных программ, например компьютерных игр, компьютерных шрифтов работает с такими кривыми, даже и не подозревая об этом. И тем не менее справедливее было называть эти кривые кривыми Бернштейна— Безье.

Справка

Параметрическое представление функции — это выражение функциональной зависимости между несколькими переменными введением вспомогательных переменных, которые принято называть "параметрами". Если мы располагаем двумя переменными, например по оси х и по оси у, то зависимость между ними можно рассматривать как уравнение плоской кривой. Например, координаты х и у точек этой кривой определяются каким-то параметром, скажем, величиной t, которую определяют как некоторый диапазон. Особенно важно такое представление для пространственных кривых, поскольку обеспечивает более легкий способ построения графиков.

Применение параметрических функций позволяет применять более сложные функции, а не только линейную аппроксимацию, поскольку одним из основных недостатков аппроксимации прямыми является, как уже указывалось, наличие угловых изгибов, которые даже при относительно невысоком увеличении не создают впечатления гладкости. Поэтому неизбежной заменой прямолинейным сегментам могут быть только кривые, которые способны обеспечить требуемую гладкость (забегая вперед, можно указать, что речь идет о кривых Безье и NURBS-кривых). Но сначала необходимо более точно определить понятие гладкости.

Свойства кривых Безье

Кривые Безье любой степени обладают следующими важными свойствами. П Начальная и конечная контрольные точки лежат на кривой.

Кривая на всем протяжении непрерывна, у нее отсутствуют разрывы. Это важнейшее свойство, без которого кривая Безье вообще бы не рассматривалась.
Касательные к кривой в начальной и конечной контрольных точках являются отрезками, соединяющими их с другими двумя соседними контрольными точками, через которые в общем случае кривая не проходит.
Точки на краях касательных будут располагаться на кривой только в том случае, если последняя представляет собой прямую линию.
Поскольку кривая Безье представляет собой взвешенное усреднение всех ее контрольных точек с положительными весами, а сумма их равна единице, кривая всегда располагается внутри выпуклого многоугольника из ее контрольных точек (рис. 12.20), как и рассмотренная выше NURBS-кривая.

Типы опорных точек

Соединительные точки между сегментами бывают нескольких типов. Действительно, можно предположить, что в одном случае требуется обеспечить соединение, скажем, криволинейного сегмента с прямым, в другом случае получить идеально гладкое сочленение (сопряжение), т. е. без стыка или перегиба.

В качестве образцов опорных точек составим таблицу для следующих векторных программ, использующих кривые Безье: CorelDRAW, Adobe Illustrator и Macromedia FreeHand.

Узлы

На рис. 12.10 все базовые функции имеют одинаковую форму и размещены на равных расстояниях друг от друга. Это очень симметрично и элегантно, но на самом деле желательно варьировать длины интервалов таким образом, чтобы определенные контрольные точки влияли на значительно больший сегмент кривой, а определенные — на меньший. Это создает условие для неоднородности (Non-Uniform) в описании кривой.

Однако определение последовательности точек, на которые разбивается ось параметра t, является не очень легкой задачей. Ведь при изменении относительных интервалов между такими точками, вам представится возможность менять длительность воздействия контрольных точек на движущуюся вдоль кривой частицу.

Точки, разграничивающие интервалы, получили название узлов (knots), а их упорядоченный список — название узлового вектора (knot vector).

Узловой вектор базовой функции, представленный на рис. 12.11, имеет вид {0.0, 1,0, 2.0, 3.0, 4.0, 5.0, 6.0, 7.0}.

Это пример однородного узлового вектора (uniform knot vector), в котором все функции определены на одинаковых временных интервалах.

Векторный формат AI

Векторный формат AI принадлежит фирме Adobe и является внутренним форматом векторного редактора Adobe Illustrator.

Векторный формат CDR

Векторный формат CDR принадлежит фирме Corel и является внутренним форматом векторного редактора CorelDRAW.

Векторный формат EPS

Векторный формат EPS (Encapsulated PostScript) является вариантом PostScript-файла. Он разработан фирмой Adobe Systems как универсальный формат для нужд цифровой графики и полиграфии.

Изображение в файле хранится в двух вариантах (как в формате TIF): основной вариант — это собственно векторное изображение, сохраненное как

описание на языке PostScript, и дополнительный вариант — это пиксельное изображение с уменьшенным разрешением, используемое (так же, как и в формате TIF) для предварительного просмотра. Кроме того, в программах верстки пиксельное изображение отображается на экране и печатается на принтерах, не поддерживающих язык PostScript (разумеется, со всеми вытекающими из этого последствиями, на что важно обратить особое внимание).

Векторный формат FH

Векторный формат FH с порядковым номером версии принадлежит фирме Macromedia и является внутренним форматом векторного редактора FreeHand.

Резюме

Идея векторной графики состоит в описании линейных фрагментов с помошью единственной формулы.
При этом разбиение произвольных кривых на отдельные фрагменты (сегменты) разумно выполнять, учитывая следующие исходные условия: фрагменты должны быть достаточно короткими, а формула должна обеспечивать дстаточно близкую аппроксимацию кривых.
Линейная зависимость обладает важным достоинством — простотой, но при этом не лишена серьезных недостатков (объекты, составленные только из прямолинейных сегментов, лишаются возможности произвольного масштабирования, для достоверной аппроксимации формы объекта потребуются десятки тысяч линейных сегментов).
Поэтому неизбежной заменой прямолинейным сегментам могут быть только кривые, которые способны обеспечить требуемую гладкость (речь идет о кривых Безье и NURBS-кривых).
Если обращаться к уравнениям со степенью выше первой, следует признать, что явный способ представления не .может применяться там, где требуется описание произвольных кривых, размещаемых в произвольных местах на плоскости.
Альтернативным способом описания кривой является определение кривой как параметрической сплайновой функции.
Одной из основополагающих особенностей NURBS-кривой является то, что ее форма определяется расположением множества контрольных точек (control points). Она позволяет локализовать изменение формы кривой перемещением отдельных контрольных точек без изменения формы кривой в целом.
Рациональные кривые обладают двумя дополнительными свойствами (они обеспечивают корректный результат при проекционных трансформациях (например, масштабировании), их можно использовать для моделирования кривых любого вида, включая конические сечения).
При всех своих выдающихся свойствах NURBS-кривые все же обладают существенным недостатком: расширенные возможности не могли не сказаться на сложности и на уровне инструментария для их построения, а это, в свою очередь, требует от дизайнера повышенных условий для его освоения, не говоря уже о необходимости определенного уровня математической подготовки.
Кривые Безье получили широкое распространение, т. к. обладают следующими важными свойствами (начальная и конечная контрольные точки лежат на кривой, кривая на всем протяжении непрерывна, у нее отсутствуют разрывы, касательные к кривой в начальной и конечной контрольных точках являются отрезками, соединяющими их с двумя другими соседними контрольными точками).
Для построения кривой Безье требуются четыре контрольных точки, хотя кривая физически проходит только через две из них (опорные точки). Две точки остаются в стороне (управляющие точки).
Соединительные точки между сегментами бывают нескольких типов, что позволяет обеспечить различные формы соединения (гладкую, тангенциальную или на изгиб).
Язык описания страницы PostScript, созданный как язык управления графическими устройствами, решает задачи передачи информации между прикладными программами (графическими редакторами, программами верстки) и устройствами визуализации (лазерными принтерами, фотонаборными автоматами и цифровыми офсетными машинами).
Последующее развитие языка PostScript не изменило своей основы и продолжает идти по пути интегрирования новых возможностей выводных устройств (цветная печать, системы управления цветом и т. д.).
Каждая векторная программа обладает собственным графическим форматом, между этими форматами нет однозначного соответствия, поэтому конвертирование одного формата в другой сопряжено с многочисленными погрешностями, особенно в последнее время, когда векторные программы насыщены разнообразными эффектами.

В следующей главе рассматриваются основы самого сложного направления векторной графики — трехмерной графики. Если трехмерная графика не является областью ваших интересов, вы просто можете перейти к части V, в которой предлагается сравнение пиксельной и векторной графики, а также их взаимные переходы.

Векторный формат PDF

Векторный формат PDF (Portable Document Format — "переносимый формат документов") — это еще одна ипостась языка PostScript, а именно его оптимизированная версия, ориентированная как межплатформенный формат, интегрирующий макет страницы с иллюстрациями, как векторными, так и пиксельными, шрифтами, гипертекстовыми ссылками, звуками и анимационными фрагментами. Для обеспечения небольшого размера используются разные способы компрессии.

Язык PostScript

ЯЗЫК описания страницы PostScript был создан в начале 80-х годов прошлого века фирмой Adobe. Его идеология состояла в том, что он был призван стать языком управления графическим устройством, например лазерным принтером, а не просто выполнять узкую задачу — позиционировать только черные точки, т. е. не только создавать битовую карту изображения с учетом разрешения выводного устройства (так работает язык PCL). Главная обязанность этого языка должна заключаться в передаче информации между прикладными программами (графическими редакторами, программами верстки) и устройствами визуализации (лазерными принтерами, фотонаборными автоматами и цифровыми офсетными машинами).

Поэтому формирование полной битовой карты страницы было перенесено в обязанность принтера, что вызвало необходимость включить в его состав как вычислительный блок, так и блок памяти.

В основу языка PostScript были положены следующие условия.

Основой векторного принципа кодирования графической информации приняты кривые третьего порядка (кривые Безье). И что очень важно, эти кривые использовались для описания как графики, так и шрифта, что обусловило единые алгоритмы обработки (с некоторыми небольшими отличиями).
С самого начала было принято решение разрабатывать PostScript как язык программирования высокого уровня, а не просто язык линейного управления внешним печатающим устройством. Поэтому были предусмотрены все возможности, свойственные классическим языкам программирования, например циклы, ветвления, подпрограммы и т. д. Кроме того, очень важно отметить, что PostScript это язык интерпретирующего типа (программа обрабатывается по мере поступления команд). Файлы в формате PostScript сохраняются в виде обычных текстовых символов (первая половина кодовой таблицы ASCII), что позволяет "рисовать" страницы в обычном текстовом редакторе, сейчас, конечно, это не имеет значения, но в свое время впечатляло. Поэтому, в сущности, документ, написанный на языке PostScript или сгенерированный из какого-либо приложения, — это программа, которая подлежит выполнению, и этим "занимается" интерпретатор языка, входящий в состав принтера. Такая программа может быть совсем короткой, и ее передача на принтер займет не так много времени (чего, впрочем, нельзя сказать о ее выполнении), а может быть и очень значительной и ее передача на принтер может происходить не один час.
Изображение, которое описывается с использованием языка PostScript, никаким образом не связано с разрешающей способностью конкретных устройств вывода. Процесс приспособления изображения к возможностям принтера (процессы растеризации и растрирования) происходит уже в самом принтере, тем самым добивается максимальное качество, на которое он способен. Заранее готовить изображение, приспособленное к конкретному принтеру, нет необходимости.
С точки зрения содержания язык PostScrip — это графика, основанная на кривых Безье. Кривые Безье — это воображаемые линии, которым можно присвоить обводку (stroke) и заливку (fill). Кроме того, возможны импортирование и обработка пиксельной графики.

Эти условия и их реализация вывели язык PostScript на позиции несомненного лидера и позволили ему стать основой всей области компьютерной графики и полиграфии.

Последующее развитие языка не изменило своей основы, но шло по пути интегрирования новых возможностей выводных устройств (цветная печать, систем управления цветом и т. д.).

это значение, важность, влияние, которое

"Вес" в математическом смысле — это значение, важность, влияние, которое выражается особой функцией или числовым значением. Это одно из важных понятий в теории принятия решений.

Изначально координата w равняется единице, но при увеличении этого значения для контрольной точки увеличивается степень ее воздействия на форму кривой и последняя сильнее выгибается в сторону контрольной точки (рис. 12.15).

Такое отображение все чаще используется

Такое отображение все чаще используется и в программах пиксельной графики, а также в программах верстки.

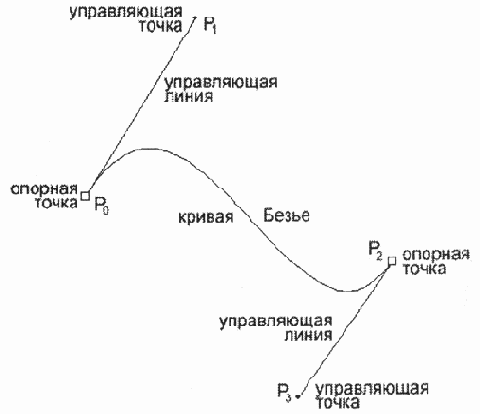
Для построения этой кривой требуются четыре контрольные точки. Но кривая физически проходит только через две из них, они получили название опорных. Одна из точек называется начальной (start point), а другая — конечной (end point). Две точки остаются в стороне, они получили название управляющих (control point).

И для того чтобы их не "потерять" (особенно когда в документе кривых насчитываются многие десятки и сотни), в программах векторной графики, да и в любых других программах, управляющие точки соединяются с опорными точками какой-нибудь линией. Иногда пунктирной, иногда тонкой сплошной.

Почему кривая располагает начальной и конечной точками? Потому что, вообще говоря, кривая Безье — это, прежде всего, вектор.

Для того чтобы отличать кривую

Для того чтобы отличать кривую как элементарную кривую, исходную кривую и кривую, которая уже находится в составе контура, последнюю чаще всего принято называть сегментом (сегментом контура или сегментом кривой).

По сути дела любая векторная конструкция (векторный контур или векторная форма) создается из векторных сегментов, каждый из которых идентичен отдельной элементарной кривой Безье.

Отсюда следует, что между ними образуются соединительные точки, которые иногда называются узлами (например, nodes — в графическом редакторе CorelDRAW). Метафора в этом случае очевидна: куски проволоки связываются узелками.

В других программах эти точки называются опорные точки (anchor point), дословно "якорные точки" (Adobe Illustrator), или просто точки (Macromedia FreeHand).

Для поддержки соотношения между элементарными сегментами существуют разные типы опорных точек.

в трехмерной графике представлены ниже

Типы опорных точек в трехмерной графике представлены ниже на примере Autodesk 3D МАХ.
Первый тип опорной точки, который соединяет два сегмента, обеспечивает независимость управляющих точек по направлению и длине друг от друга.

Такое состояние сегментов называется изгиб (рис. 12.30).

В программе CorelDRAW такая точка называется перегиб (cusp). В других программах у нее более простое имя: угловая (corner). Помимо этого, в программе FreeHand при вьщелении угловая точка обозначается квадратиком.

Угловое сочленение сегментов (изгиб) далеко не всегда разумно и выгодно. Например, для создания окружности необходимо обеспечить соединение, которое в черчении и в геометрии называют гладким сопряжением, когда одна кривая плавно переходит в другую. Такое сочленив обеспечивает гладкая опорная точка (smooth) (рис. 12.31).

Условием этого являются управляющие линии, лежащие на одной прямой У такой точки направление управляющих линий фиксировано относительно друг друга, при перемещении одной управляющей линии другая также движется синхронно как рычаг. Вместе с тем, такие управляющие линии могу] различаться по величине.

и Macromedia Freehand такой тип

В программах Adobe Illustrator и Macromedia Freehand такой тип опорной точки отсутствует, хотя его можно получить вручную.

В свою очередь, у программы FreeHand в отдельный вид опорных точек выделен случай гладкого сочленения прямолинейного и криволинейного сегментов (рис. 12.33). Такая точка получила название тангенциальной (connecter point). При выделении такая точка обозначается треугольником.

Логика этой точки заключается в следующем: для того чтобы криволинейный сегмент гладко сопрягался с прямой линией, касательная криволинейного сегмента должна совпасть с продолжением прямого сегмента. Поэтому управляющая точка криволинейного сегмента способна двигаться только вдоль этой касательной.

и Adobe Illustrator такое соединение

В программах CorelDRAW и Adobe Illustrator такое соединение также имеет место, но не выделено в специальный тип опорной точки.

Формат предполагает запись пиксельного изображения

Формат предполагает запись пиксельного изображения в форматах TIF или WMF. Если предполагается необходимость печати файла EPS на PCL-принтере, следует сохранить документ с вариантом TIFF и достаточным разрешением.

Благодаря своей надежности, совместимости со многими программами и платформами и большой совокупности настраиваемых параметров формат EPS выбирают большинство разработчиков программного и аппаратного обеспечения.

Указанные недостатки заставляют искать другие

Такой принцип по-прежнему используется, например в системах, связанных с режущими устройствами.

Указанные недостатки заставляют искать другие способы описания формы объектов и использовать более сложные кривые, в частности кривые более высоких степеней (второй, третьей и т. д.).

В 1981 году состоялась знаменитая

В 1981 году состоялась знаменитая выставка "Москва — Париж", сначала во Франции, потом — в СССР. На выставке демонстрировались шедевры русской и французской культуры конца XIX — начала XX веков. Балет, живопись, графика, скульптура, поэзия двух стран имеют очень тесные связи и взаимовлияние. Математика и техника — в том числе. Русский математик разработал довольно абстрактный математический аппарат, а затем этой "абстракции" нашлось применение в виде конкретных очертаний кузова французского автомобиля.

Заметим заранее, привычные для плоских

Заметим заранее, привычные для плоских векторных художников кривые Безье являются специальным (частным) случаем В-сплайна. Информацию о кривых Безье см. далее, в одноименном разделе.

Вряд ли эти расшифровки внесли большую ясность для читателей, не знакомых с математикой. Тогда давайте все по порядку.

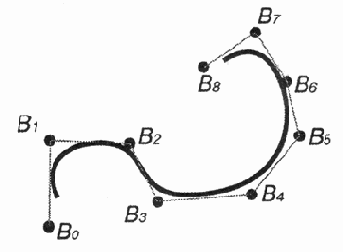
Контрольные точки соединены для наглядности

Контрольные точки соединены для наглядности прямыми линиями. Эта ломаная линия получила название управляющего многоугольника (control polygon).

Значение базовой функции представляет собой

Собственно, в названии В-сплайнов буква "В" и означает "базовые" (basis).

Значение базовой функции представляет собой вещественное число. Необходимо учесть, что описание NURBS-кривой требует задания базовой функции для каждой контрольной точки.