Численное исследование одномерных

Приведем краткое описание постановки одномерных задач для расчета установившегося распределения концентрации Rn, выходящего из почвы в атмосферу.

Рассматриваются задачи о заполнении радоном первоначально пустого слоя, состоящего из 2-х однородных сред: от –z0 до z = 0 – грунт с пористостью m, от 0 до z1 – воздух (рис.7).

Рис.7. Геометрия задачи.

При описании распределения радона в средах используется одномерное конвективно-диффузионное уравнение:

Основные параметры задачи:

коэффициент диффузии радона в грунте D1=0.05 см2/с,

коэффициент диффузии радона в воздухе D2=0.1 см2/с,

постоянная полураспада радона l=2.1×10-6 с-1,

пористость грунта m=0.2,

размеры рассматриваемой области z0=9м, z1=3м.

Здесь индекс 1 относится к грунту, а индекс 2 – к воздуху.

Данная задача рассматривалась в нескольких постановках:

· моделировался выход радона из грунта в атмосферу только за счет диффузии, когда в грунте действовал внутренний источник радона Q=lC0, равномерно распределенный по всей глубине (вариант 1);

· моделировался выход радона как в варианте 1, когда на глубине от 0 до 1 м не выделялся радон (вариант 2 - имитируется засыпка);

· моделировался выход радона из грунта в атмосферу как в варианте 1, когда в пределах грунта задан поток воздуха по проницаемым каналам с постоянной скоростью u1=const (вариант 3);

· моделировался выход радона из грунта в атмосферу как в варианте 2, когда в пределах грунта задан поток воздуха с постоянной скоростью u1=const (вариант 4).

Вариант 1.

В варианте 1 моделировался выход радона из грунта в атмосферу только за счет диффузии (u1=u2=0 ) и внутреннего источника Q=lC0, равномерно распределенного во всем слое грунта. На границе z = –z0 задано граничное условие

, т.е. концентрация радона поддерживается на постоянном уровне за счет внутренних источников.
На границе z = z1 для моделирования свободной поверхности (ухода радона в атмосферу) величина CRn берется с предыдущего шага. При этом, в начальный момент (t=0) во всей счетной области CRn = 0. Для получения установившегося распределения радона, счет велся до выхода на стационарное решение.

Вариант 2.

В варианте 2 моделировался выход радона из грунта в атмосферу за счет диффузии, когда в грунте действовал внутренний источник радона Q=lC0, равномерно распределенный по всей глубине до 1 метра от поверхности, а на глубине от 0 до z2=1 м - грунт не выделяет радон. Граничные и начальные условия те же, что и в варианте 1.

Для удобства изображения приведем профили концентрации в относительных единицах С=CRn/C0. Пространственное распределение установившейся концентрации радона CRn(z)/C0 и временная зависимость CRn(t)/C0 в точке раздела сред (z=0) для вариантов 1,2 представлены на рис.8,9.

Рис.8. Пространственное распределение концентрации радона CRn(z)/C0 в вариантах 1,2 (z2 – толщина засыпки).

Из рис.8 видно, что во 2 варианте с метровой засыпкой выход радона из грунта в атмосферу примерно в два раза меньше чем в 1 варианте без засыпки.

Рис.9. Временная зависимость CRn(t)/C0 в точке раздела сред (z=0) в вариантах 1,2

(z2 – толщина засыпки).

Из рис.9 видно, что примерно через 40 суток на границе раздела сред устанавливается постоянное значение концентрации СRn. В первом случае СRn/C0»0.14, а во втором СRn/C0»0.06. Видно, что засыпка нейтральным грунтом сильно влияет на концентрацию радона при выходе в атмосферу.

Вариант 3.

В варианте 3 моделировался выход радона из грунта в атмосферу как в варианте 1, когда в пределах грунта задан поток воздуха по проницаемым каналам с постоянной скоростью u1=const .

В данном варианте моделировался выход радона из грунта в атмосферу, когда в грунте задавался поток воздуха, выходящий по проницаемым каналам с постоянной скоростью u1=0.001см/с и внутренний источник радона Q=lC0. В воздухе распространение радона происходит только за счет диффузии (u2=0).

Граничные и начальные условия те же, что и в варианте 1.

Вариант 4.

В варианте 4 моделировался выход радона как в варианте 3, когда на глубине от 0 до z2=1м грунт не выделяет радон.

Пространственное распределение установившейся концентрации радона CRn(z)/C0 и временная зависимость CRn(t)/C0 в точке раздела сред (z=0) для вариантов 3,4 представлены на рис.10,11.

Рис.10. Пространственное распределение концентрации радона в вариантах 3,4

(z2 – толщина засыпки).

Из рис.10 видно, что в 4 варианте с метровой засыпкой выход радона из грунта в атмосферу примерно в полтора раза меньше чем в 3 варианте без засыпки.

Рис.11. Временная зависимость концентрации радона в точке раздела сред (z=0) в вариантах 3,4 (z2 – толщина засыпки).

Из рис.11 видно, что примерно через 60 суток на границе раздела сред устанавливается постоянное значение концентрации СRn. В первом случае СRn/C0 »0.5, а во втором СRn/C0 »0.4. Видно, что моделирование конвективного переноса радона сильно влияет на концентрацию радона при выходе в атмосферу.

После описания распределения концентрации Rn, выходящего из почвы в атмосферу, были проведены расчеты для установления распределения CRn по глубине для различных значений D2.

Основные параметры задачи: коэффициент диффузии в воздухе D2=0.1 см2/с, коэффициент диффузии в грунте варьировался D1={0.1, 0.05, 0.01} см2/с, пористость грунта m=0.2, постоянная полураспада радона l=2.1×10-6 с-1, z0=9м, z1=9м. В грунте действовал внутренний источник радона Q=l, равномерно распределенный на глубине от -z0 до -1м. Моделировался выход радона только за счет диффузии, т.е. скорость конвективного переноса u1=u2=0. При этом, в начальный момент (t=0) во всей счетной области CRn = 0, на границе z = –z0 было задано граничное условие ¶CRn(z=–z0,t)/ ¶z=0, а на границе z = z1 для моделирования свободной поверхности (ухода радона в атмосферу) величина CRn бралась с предыдущего шага. Полученные зависимости CRn(z) были нормированы на экспериментальное значение CRn в точке z=0.

Данные эксперимента представлены в таблице 5

( здесь следует отметить, что ПДК по радону – 200 Бк/м3).

Таблица 5.

Z(cm)	CRn (Бк/м3)
0	970
20	720
50	380
200	360

На рис.12 представлено установившееся распределение CRn по z для различных значений D1.

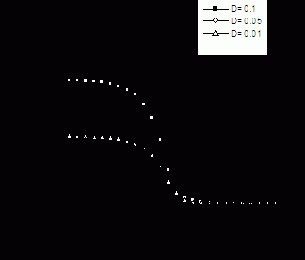
Рис.12. Распределение CRn для различных значений D1

Из рис.12 видно, что при уменьшении D1 на порядок концентрация радона в грунте уменьшается в 2 раза.

На рис.13 представлено установившееся распределение CRn по z при D1=0.1 см2/с для различных значений u1.

Рис.13. Распределение CRn для различных значений u1.

Из рис.13 видно, что при увеличении u1 на порядок концентрация радона в грунте уменьшается в 7 раз.

На рис.14 приведено сравнение установившегося распределения CRn в выделенном приповерхностном участке zÎ[0,220cm] для различных значений D1 и экспериментальных данных из таблицы 5.

Рис.14. Распределение CRn для различных значений D1.

На рис.15 представлены установившееся распределение CRn в выделенном приповерхностном участке zÎ[0,220cm] для различных значений u1 и экспериментальные данные из таблицы 5.

Рис.15. Распределение CRn для различных значений u1.

Из рисунков 14,15 видно, что в двух точках существует разница между результатами расчетов и экспериментальными данными. Разница, по-видимому, объясняется погрешностями измерений.

Рассмотрим результаты трехмерных численных расчетов по изучению радонового поля над хвостохранилищем. Цель этих расчетов состояла в определении пределов распространения вредной для здоровья концентрации радона. В этих задачах использовались экспериментальные данные измерений радиационного фона. Расчетная область совпадает с областью вокруг ХВХ, где проводились измерения гамма-фона. Первая задача - это задача на установление стационарного распределения радона над площадью хвостохранилища в безветренную погоду.Эти расчеты при отсутствии ветра позволяют оценить характерную высоту облака с его повышенным содержанием, подобрать коэффициенты модели, соответствующие изучаемому региону. Вторая задача - это исследование распределения радона над хвостохранилищем при постоянном ветре. Эти расчеты позволяют оценить количество радона, уносимого ветром с площади хвостохранилища.

Численное исследование распределения радона над хвостохранилищем при постоянном ветре

После исследования задачи на установление стационарного распределения радона в неподвижной атмосфере необходимо рассмотреть динамику сноса радонового поля из области хвостохранилища постоянным ветром в каком-либо направлении.

Пусть в начальный момент t=0 над хранилищем имеет место стационарное распределение Rn по высоте. В этот же момент включается ветер в направлении X. В ходе решения нестационарной проблемы переноса определялся темп спада максимальной концентрации Rn в приземном слое Сmax. В ходе счета достигается режим установления, когда Сmax(x,y,t) приближается к фоновому значению. Исходя из расчетного темпа спада Сmax, оценивается время исчезновения повышенной концентрации Rn при постоянном ветре. При линейной модели переноса такая же концентрация установится через несколько часов над населенными пунктами в окрестности ХВХ. Но постоянная смена ветра и вертикальная конвекция приводит к быстрому снижению концентрации радона в воздухе. Экспериментальные данные говорят о концентрациях ниже ПДК за санитарной зоной и практическом отсутствии радона в районе жилых массивов.

На рис.22 представлено установившееся распределение CRn

на поверхности ХВХ (z=0.5 см, u=1 м/с).

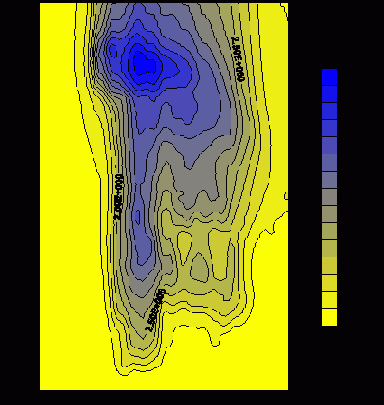
Рис.22. Распределение CRn (10-2nKu/m3) на поверхности ХВХ (z=0.5 см).

На рис.23 представлено установившееся распределение CRn

над поверхностью ХВХ (z=20 см, u =1 м/с).

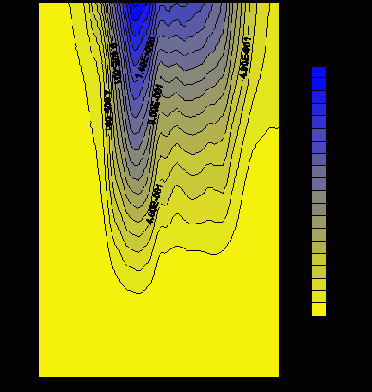
Рис.23. Распределение CRn (10-2nKu/m3) над поверхностью ХВХ (z=20 см).

На высоте одного метра концентрации CRn практически не наблюдается.

На рис.24 представлено распределение средней по высоте концентрации Cs.

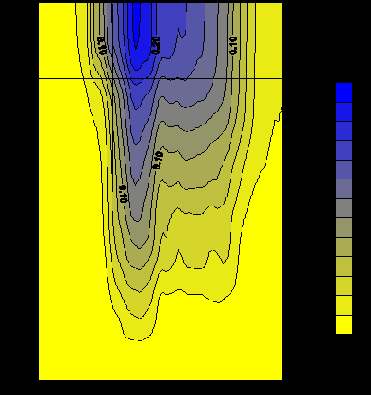
Рис.24. Распределение средней по высоте концентрации Cs(10-2nKu/m3).

На рис.25 представлено установившееся распределение CRn

над поверхностью ХВХ (z=0.5 см) в трехмерном виде, где в горизонтальной плоскости отложены координаты поверхности ХВХ, а по вертикали - значения концентрации.

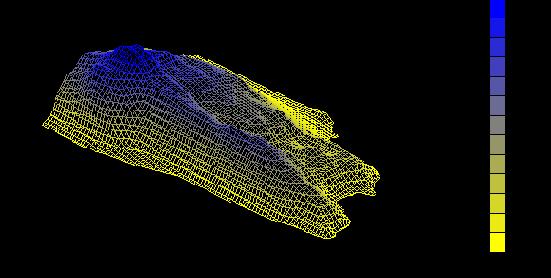
Рис.25. Распределение CRn

(10-2nKu/m3) над поверхностью ХВХ.

На рис.26 для продольного сечения при х=x0=594 м представлены в относительных единицах зависимости

.
Продольное и поперечное сечения, выбранные для анализа результатов, изображены вертикальной и горизонтальной линиями на рис. 24.

Рис.26. Зависимости

для продольного сечения.

На рис.27 для поперечного сечения при y=y0=2398 м представлены зависимости

Рис.27. Зависимости

для поперечного сечения.

В результате решения данной задачи получены следующие интегральные характеристики:

интегральная концентрация по всему пространству над ХВХ - C=0.00001 Ku;

коэффициент корреляции радонового поля и гамма-фона - k=0.45;

дисперсия распределения радона по площади хранилища

=0.0006 (nKu/m3).

Численные расчеты показали, что между мощностью дозы g-излучения и содержанием Ra над хранилищем при постоянном ветре наблюдается достаточно сильная корреляция.

Численное исследование ширины перемешивания радона и воздуха при различных скоростях ветра

При изучении процесса распространения радона воздушным путем возникает задача подъема радона в атмосферу за счет турбулентного перемешивания. В процессе

смешения двух газов, радона и воздуха, скользящих друг по другу под действием ветра, образуется зона перемешивания, ширина которой зависит от отношения скорости воздуха к скорости радона. Для изучения ширины перемешивания радона с воздухом при различных скоростях ветра рассмотрена задача на сдвиговую неустойчивость двух газов, радона и воздуха, по

- модели из комплекса KIVA (Amsden A.A., O’Rourke, Butler T.D. A Computer Program for Chemically Reactive Flows with Sprays. LA-11560-MS, UC-96, 1989).

При моделировании перемешивания для упрощения будем считать, что поверхность над хвостохранилищем состоит из двух газов разделенных горизонтальной границей в поле силы тяжести. Толщина нижнего слоя (радона) 0.5м, а верхнего (воздуха) 1.5м (рис. 28). Будем следить за фрагментом поверхности над хвостохранилищем длинной 100м. На левую границу набегает поток до 0.5 метров имеющий скорость и плотность

, а от 0.5м до 2м –

. Уравнения состояния газов задаются в виде

, где

–квадрат скорости звука.

Рис. 28. Геометрия и краевые условия задачи.

Плотность воздуха полагалась

, плотность радона

, скорость звука

. На границе разделов веществ (X=0) скорость полагалась равной «эффективной» скорости, которая бралась в виде

. Расчет проводился до установления стационарного режима

, что соответствует примерно 3.8 суток (время полураспада радона). Отметим, что стационарный режим, т.е. когда ширина перемешивания не меняется с течением времени, наступает раньше

. Для расчета было взято равномерное разбиение по

и по

. На левой границе было реализовано граничное условие притока вещества, а на правой оттока.

В таблице 6 приведены параметры потоков для 3 вариантов. Скорость радона полагалась

а скорость воздуха

бралась

, что соответствует средней скорости ветра по розе ветров Кара-Балты. В столбце

приведена максимальная ширина перемешивания воздуха и радона в метрах.
В столбце

приведена разница в высоте радона с концентрацией 0.001 и начальной высотой (0.5 м).

Таблица 6

Номер численного эксперимента
Вариант 1	100	200	0.044	0.008
Вариант 2	100	400	0.052	0.012
Вариант 3	100	800	0.063	0.021

На рис. 29 приведены фрагменты системы (на рис. 28 он отмечен черным прямоугольником): по вертикали от 0.455 м до 0.545 м и 0.1 м по горизонтали, для трех вариантов расчета, а также распределение массовой концентрации радона

, где

-полная масса смеси газов в ячейке, а

– масса радона в ячейке на конечный момент времени

Черная изолиния сверху соответствует минимальной массовой концентрации радона 0.001, а внизу максимальной – 1. Пунктирная линия соответствует начальному положению радона.

Вариант 1 Вариант 2 Вариант 3

Рис. 29. Распределение массовых концентраций радона для трех вариантов расчета на момент установления

Численные расчеты по математической программе

турбулентного перемешивания показывают, что сдвиговая

неустойчивость слабо развивается при тех скоростях, которые характерны для района ХВХ. Однако, несмотря на упрощенный подход к моделированию перемешивания радона и воздуха над хвостохранилищем, следует отметить, что:

1.      с увеличением скорости ветра рост зоны перемешивания возрастает нелинейно;

2.      при рассмотренных скоростях ветра (от 2м/сек до 8/м.сек) зона перемешивания воздуха и радона составляет от 1 до 2 см, что составляет 1.6%-4% от начальной толщины слоя радона.

Приведенные расчеты являются предварительными. Предложенная модель является неполной, т.к. не учитывается тепловая конвекция газов при прогреве поверхности, а также развитие турбулентности от неровности поверхности, так называемая турбулентность от пограничного слоя. Кроме того, требуют уточнения некоторые данные, например, плотность радона, средняя температура газов, распределение радона на поверхности по высоте.

Для верификации модели необходимы эксперименты по измерению концентрации радона при различных скоростях ветра и на разных высотах. Реализация полной модели турбулентного перемешивания достаточно трудоемка и выходит за рамки данного проекта.

Из анализа всех численных исследований можно сделать следующие выводы:

1.      При отсутствии ветра происходит радиактивное загрязнение только района ХВХ.

2.      При любом ветре радиактивное загрязнения окружающей местности не происходит, т.к. концентрация радона очень быстро падает за счет перемешивания с воздухом.

3.      Перемешивание происходит в основном за счет процессов конвекции. Сдвиговая

неустойчивость слабо развивается при тех скоростях, которые характерны для района ХВХ.

4.      Выбор места для организации хвостохранилища вблизи жилых массивов не сказывается негативно в той же степени, как при рассмотрении загрязнения от переноса пыли с территории ХВХ или грунтовыми водами.

5.      Возможно радиоактивное облучение при попадании людей на территорию ХВХ.

6.      Желательно произвести засыпку ХВХ метровым слоем грунта и охранять территорию ХВХ от проникновения туда населения.

Численное исследование задачи

Полевые эксперименты показали, что между мощностью дозы g-излучения и содержанием Ra в подпочвенном слое хранилища наблюдается четкая линейная зависимость:

. Максимальное измеренное значение мощности дозы составляет g ~ 1000 мкр/ч, а соответствующая ей концентрация радия (в единицах активности) CRa ~ 0.8 nKu/г; в результате имеем оценку kg,Ra ~ 0.0008 nKu ×ч/г×мкр.

С использованием этой линейной зависимости можно определить источник радона в уравнении конвективно-диффузионного переноса в области грунта:

, Qz = 1 при z < 0 и Qz = 0 при z ³ 0,

где rп – плотность породы, равная примерно ~ 2.5г/см3, ERn – коэффициент эманирования по радону; для вторичных (переработанных) пород, к каковым относится высохшая пульпа, содержащая радий, ERn

оценивается ~ 0.3 – 0.5.

Значения мощности дозы g

- излучения измерены по всей площади хвостохранилища и проинтерполированы на декартову сетку с размером ячейки DX = DY ~ 30м.

В результате уравнение конвективной диффузии записывается в виде:

Исходя из этого уравнения, сформулируем задачу на установление следующим образом:

1. Рассмотрим чисто диффузионный процесс -

2. Счетная область является параллелепипедом, характеризуемым координатами граничных точек Xmin=0, Xmax=1950м; Ymin=0, Ymax=3006м; Zmin= - 4м, Zmax= 4м.

3. Размер ячейки в плоскости XOY определяется дискретизацией g- фона и составляет 31´31м2. По оси Z количество точек, предположительно, должно быть ~ 20 в грунте и ~ 40 в воздухе; в силу принципиальной неоднородности распределения CRn в вертикальном направлении эти точки сгущаются вблизи границы грунт – воздух.

4. В начальный момент времени считаем, что во всей счетной области CRn(t=0,x,y,z)=0.

5. Граничные условия:

а) на границе z= Zmax величина CRn в каждый момент времени берется с предыдущего шага;

б) на нижней границе z= Zmin – ставится условие непроницаемости

;

в) на 4-х боковых границах в плоскости XOY – ставится также условие непроницаемости

.

6. Параметры уравнения: ux=uy=0, D=10-6м2/с, пористость m=0.2 .

7. Счет велся до установления стационарного решения; по диффузионным оценкам момент установления tкон ~ 106 – 107с.

В результате решения определялись следующие интегральные характеристики:

средняя концентрация по вертикали от поверхности земли до высоты h=4 м

;

средняя концентрация по всему пространству над хвостохранилищем до высоты h=4 м

;

коэффициент корреляции радонового поля и гамма-фона

, где

;

дисперсия распределения радона по площади хранилища

.

На рис.16 представлено установившееся распределение CRn

на поверхности хранилища (z=0.5 см).

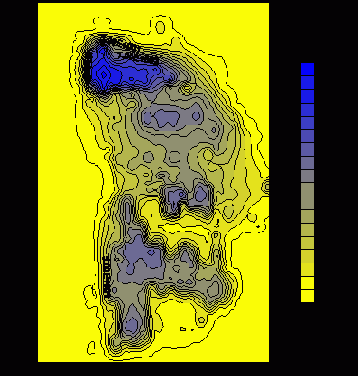
Рис.16. Распределение CRn (10-2 nKu/m3) на поверхности хранилища.

На рис.17 представлено установившееся распределение CRn

над поверхностью ХВХ (z=2м).

Рис.17. Распределение CRn (10-2nKu/m3) над поверхностью хранилища (z=2 м).

На рис.18 представлено распределение средней по высоте концентрации

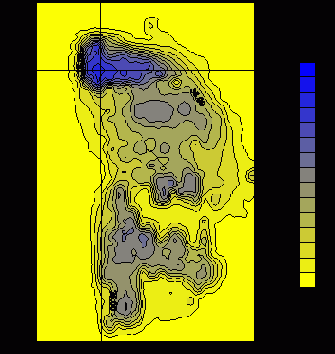
Рис.18. Распределение средней по высоте концентрации Cs(10-2nKu/m3).

На рис.19 представлено установившееся распределение CRn

над поверхностью ХВХ (z=0) в трехмерном виде, где в горизонтальной плоскости отложены координаты поверхности ХВХ, а по вертикали - значения концентрации.

Рис.19. Распределение CRn

(10-2nKu/m3) над поверхностью ХВХ.

При представлении результатов расчетов для дополнительной наглядности имеет смысл рассмотреть также одномерные распределения концентрации радона в некоторых характерных сечениях в продольном и поперечном направлениях. Подобные сечения, проходящие через область с максимальным уровнем g-фона и, соответственно, с максимальным значением CRn, изображены вертикальной и горизонтальной линиями на рис. 18. Продольное сечение в выбранной счетной области отвечает координате x0=594 м по оси OX, а поперечное сечение – координате y0=2398 м по оси OY. Графики одномерных распределений концентрации радона и g-фона в относительных единицах

, где

, приведены на рис.20, 21.

Рис.20. Зависимости

для продольного сечения.

Рис.21. Зависимости

для поперечного сечения.

Данные зависимости демонстрируют, что пространственные изменения CRn практически совпадают с аналогичными изменениями g-фона, что является следствием относительно малого времени жизни атомов радона и медленного характера их диффузионного распространения в неподвижной атмосфере от места эксхаляции (за четверо суток они диффундируют на расстояния не более 20 метров). Результирующий коэффициент корреляции для безветренной погоды оказывается близок к единице: k ~ 0.9 (почти стопроцентная корреляция).

Полное расчетное установившееся количество радона в приземном слое над ХВХ составило C = 0.004 Ku, что соответствует средней концентрации C/h×S ~ 0.5 (nKu/m3). Дисперсия распределения радона по площади хранилища получилась сравнимой с этой величиной -

~ 0.19 (nKu/m3), что также свидетельствует о слабом влиянии диффузионного переноса на распределение радона в плоскости земли.

Численные расчеты

Исходные данные и результаты оценки потерь почвы приведены в табл. 1-3.

Таблица 1. Результаты расчетов размывания ХВХ без учета климатических условий.

Месяц	p1	p2	p1/(p1+p2)	t, Н/м2	Кол-во дней с Uе ³ 8 м/с	Uе в учетные дни, м/с	Потеря Q, кг/м2	Потеря Q, мм
Январь	0,5	0,1	0,833	0,320	2,5	8,1	0,004	0,003
Февраль	0,5	0,1	0,833	0,590	5	11,0	0,418	0,321
Март	0,5	0,1	0,833	0,568	17,5	10,8	1,226	0,943
Апрель	0,5	0,1	0,833	0,527	15	10,4	0,717	0,552
Май	0,5	0,1	0,833	0,487	15	10,0	0,469	0,361
Июнь	0,5	0,1	0,833	0,600	20	11,1	1,820	1,400
Июль	0,5	0,1	0,833	0,547	15	10,6	0,873	0,671
Август	0,5	0,1	0,833	0,855	10	13,25	3,750	2,885
Сентябрь	0,5	0,1	0,833	0,395	5	9,0	0,042	0,033
Октябрь	0,5	0,1	0,833	0,955	2,5	14,0	1,343	1,033
Ноябрь	0,5	0,1	0,833	0,395	7,5	9,0	0,063	0,049
Декабрь	0,5	0,1	0,833	0,702	5	12,0	0,896	0,689
Суммарные потери за год	11,621	8,939

Таблица 2. Результаты расчетов размывания ХВХ с учетом климатических условий.

Месяц	p1	p2	p1/(p1+p2)	t, Н/м2	Кол-во дней с Uе ³ 8 м/с	Uе в учетные дни, м/с	b	Условия	Потеря Q, кг/м2	Потеря Q, мм
Январь	0,5	0,1	0,833	0,320	2,5	8,1	0	снежный покров	0	0
Февраль	0,5	0,1	0,833	0,590	5	11,0	0	снежный покров	0	0
Март	0,5	0,1	0,833	0,568	17,5	10,8	0,5	дождь	0,613	0,472
Апрель	0,5	0,1	0,833	0,527	15	10,4	0,5	дождь	0,359	0,276
Май	0,5	0,1	0,833	0,487	15	10,0	1		0,469	0,361
Июнь	0,5	0,1	0,833	0,600	20	11,1	1		1,820	1,400
Июль	0,5	0,1	0,833	0,547	15	10,6	0,5	трава	0,436	0,336
Август	0,5	0,1	0,833	0,855	10	13,25	0,5	трава	1,875	1,442
Сентябрь	0,5	0,1	0,833	0,395	5	9,0	0,5	трава	0,021	0,016
Октябрь	0,5	0,1	0,833	0,955	2,5	14,0	0,5	дождь	0,671	0,516
Ноябрь	0,5	0,1	0,833	0,395	7,5	9,0	1		0,063	0,049
Декабрь	0,5	0,1	0,833	0,702	5	12,0	0	снежный покров	0	0
Суммарные потери за год	6,327	4,867

По математической программе МИФ была проведена серия одномерных, двумерных и трехмерных численных расчетов. В одномерном случае проведены численные расчеты на получение стационарного распределения концентрации радона на стыке подпочвенного и приземного слоев. В одномерных расчетах установившегося распределения концентрации Rn, выходящего из почвы в атмосферу, проведено исследование методики на точность и выбрана разностная сетка по вертикали. Проведены сравнения с аналитическими решениями и с экспериментальными данными. Эти расчеты при отсутствии ветра позволяют оценить характерную высоту облака с его повышенным содержанием, подобрать коэффициенты модели, соответствующие изучаемому региону.

После этого были проведены двумерные и трехмерные численные расчеты для изучения радонового поля над хвостохранилищем. Цель этого этапа моделирования состоит в определении теоретических пределов распространения вредной для здоровья концентрации радона, а также нахождение метеорологических условий, наиболее способствующих распространению радона.

По одномерной программе УРАН был проведен ряд расчетов с параметрами: L=1м, l=0 сут-1, , 0 £ x £ 1 м, 0 £ t £ 50 лет. Коэффициенты D=8.0·10-5cм2/cут, D4=4.0·10-6cм2/cут, D5=0.08, Kd1=260см3/г, Kd2=50 см3/г, Kd3=500 см3/г, g=10-2 сут-1, b(C3)=bmax–C3(bmax–bmin)/C3max, C3max=300мг/л, bmax= =0.45·10-1 сут-1, bmin=0, a=7.7·10-7 сут-1, v1=v(t)/(Kd1·g) cм/cут, v2=v(t)/(Kd2·g) см/сут, g=1.1 см3/г, f=5·10-5 сут-1. v(t)=vmax–t(vmax–vmin)/tmax, vmax=400, vmin=200. Граничные условия на верхней границе: С1=6.0, С2=12, С4=21мг/л, С5=0.5 мг/л, на нижней границе: С1=C1n, С2=C2n, С4=C4n.

На рис. 34-37 приведена зависимость полученных концентраций от глубины на моменты времени t=1год, 15 лет,50 лет (с 1955г. по 2005 г.).

Рис. 34. Профили концентраций С1, С2, С3, С4 и суммарной концентрации С через 1год.

Рис. 35. Профили концентраций С1, С2, С3, С4 и суммарной концентрации С через 15 лет.

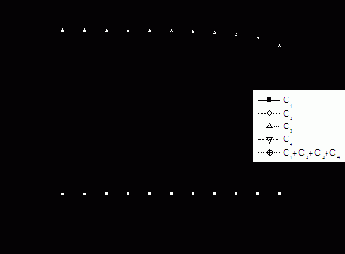
Рис. 36. Профили концентраций С1, С2, С3, С4 и суммарной концентрации С через 50 лет.

Рис. 37. Профили концентраций С1, С2, С4 через 50 лет.

На рис. 38-40 приведена зависимость полученных концентраций от времени в точке x=1м.

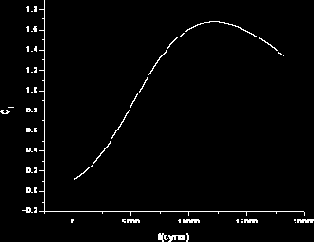
Рис. 38. Зависимость С1 от времени в точке x = 1 м.

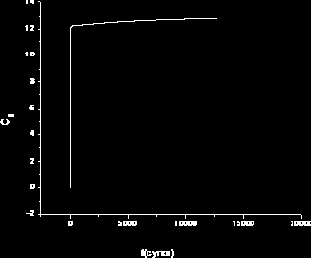
Рис. 39. Зависимость С2 от времени в точке x = 1 м.

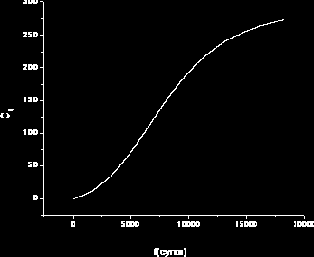
Рис. 40. Зависимость С3 от времени в точке x = 1 м.

Согласно расчетам и построенным на их основе графиков очевидно, что анион-комплексные соединения урана с концентрацией С2 (составляющие ~ 15% от общего содержания урана, сбрасываемого с промотходами) практически за год пробивают защитный слой суглинка и далее эта форма урана в суглинке нарастает за счет концентрации С1. При этом, в основном за счет конвективного переноса, доминирующего в первые годы работы ГМЗ КГРК в виду максимального объема сбросных отходов и концентрации урана в них, происходит наиболее интенсивное смещение всех форм урана вглубь водовмещающих пород ХВХ.

В дальнейшем ввиду накопления пульпового остатка выщелоченной породы, снижения объёма и концентрации урансодержащих промстоков и, как следствие, рассредоточение стока по поверхности водовмещающих пород, интенсифицируется процесс сорбции урана породами хвостохранилища.

Численные расчеты

Рис. 34. Профили концентраций С1, С2, С3, С4 и суммарной концентрации С через 1год.

Рис. 35. Профили концентраций С1, С2, С3, С4 и суммарной концентрации С через 15 лет.

Рис. 36. Профили концентраций С1, С2, С3, С4 и суммарной концентрации С через 50 лет.

Рис. 37. Профили концентраций С1, С2, С4 через 50 лет.

На рис. 38-40 приведена зависимость полученных концентраций от времени в точке x=1м.

Рис. 38. Зависимость С1 от времени в точке x = 1 м.

Рис. 39. Зависимость С2 от времени в точке x = 1 м.

Рис. 40. Зависимость С3 от времени в точке x = 1 м.

видно, что максимальная потеря

Ореол загрязнения за год (вся поверхность подвержена дефляции).



            Из рисунка 4 видно, что максимальная потеря почвы за этот период может составить 19 т/га. При этом общая площадь поверхности, подвергшаяся загрязнению, остается прежней (около 360000 га).

            В таблице 4 приведены основные параметры ветровой эрозии почвы, полученные за один год (с 1.01.1999 по 31.12.1999) при различном моделировании размеров поверхности ХВХ, подверженной дефляции.

Таблица 4. Прогноз дефляции почвы с поверхности ХВХ за 1 год.

Площадь, подверженная дефляции (га)	61	121	181	242
Отношение площади, подверженной дефляции, ко всей площади ХВХ (%)	25	50	75	100
Площадь загрязнения (га)	360000	360000	360000	360000
Потеря почвы (т/га)	5	10	14	19
Толщина эрозийного слоя (мм)	0.4	0.7	1.1	1.5
Максимальная концентрация на загрязненной площади вне ХВХ (г/м2)	1.313	2.626	3.939	5.253

На рисунке 5 выдан ореол концентрации пыли, образующийся за 50 лет (период существования ХВХ к 2005 году). Этот прогноз основан на данных метеостанции (розе ветров) за 1999 год. Так как данные метеостанции есть только за 1999 год, они продублированы 50 раз в предположении примерно одинаковой ежегодной розы ветров. То есть в каждый рассматриваемый год принимается, что основное направление ветров аналогично розе ветров за 1999 год.

Рис.5. Ореол загрязнения за 50 лет (дефляции подвержено 25% поверхности).

Из рисунка 5 видно, что максимальная потеря почвы за этот период может составить 240 т/га. При этом общая площадь поверхности, подвергшаяся загрязнению, составляет более 800 000 000 га.

При анализе результатов, необходимо отметить следующий факт. В используемой модели присутствует параметр Uкр.

– критическая скорость, при которой начинается безвозвратный перенос частиц. В ряде работ этот параметр выбирается равным 8, поэтому мы, не зная характеристик почвенного состава хвостохранилища, остановились на этом же значении.

Но нам известны результаты, где

Но нам известны результаты, где для влажных почв этот параметр принимался равным 10. При таком значении параметра Uкр.

масса выдуваемой почвы сократится более чем в 3 раза. Если же критическая скорость увеличится до 12, то масса выдуваемой почвы сократится при данной розе ветров более чем в 10 раз.

Из анализа численных исследований распространения загрязнения с поверхности ХВХ ветром можно сделать следующие выводы:

1.      Выбор места для организации ХВХ неудачен. Даже при слабом ветре пылевое загрязнение окружающей местности было предопределено;

2.      Загрязнение распространяется на площади более 1000 км2. Через 50 лет после начала эксплуатации ХВХ (к 2005 году) пылевое загрязнение распространяется на сотни километров во все стороны, на севере подходит к реке Чу, на востоке к г. Бишкек, и захватывает все окрестные районы жилых массивов;

3.      Для уменьшения площади загрязнения необходимо полное покрытие поверхности ХВХ любой растительностью.

Краткий обзор сайтов в ИНТЕРНЕТ по радиационной экологии

За весь период выполнения проекта были проведен анализ экологических сайтов в ИНТЕРНЕТ. Описание наиболее заслуживающих, на наш взгляд, внимания сайтов, приводится ниже.

WWW.GISA.RU

- сайт ИБРАЭ (Института безопасного развития ядерной энергетики РАН). Основные направления деятельности института:

1) тяжелые аварии (прогнозные расчеты безопасности);

2) экологическая безопасность;

3) поддержка перспективных направлений;

4) оперативная поддержка и аварийное реагирование;

5) информационные системы СКЦ (ситуационно – кризисного центра).

По экологической безопасности осуществляются:

· разработка методологии оценки экологических рисков;

· накопление данных;

· проведение системного анализа экологических рисков.

ИБРАЭ создает базы данных:

· размещение отходов (по отраслям и субъектам РФ);

· смертность по причинам (по отраслям и субъектам РФ);

· загрязнение атмосферного воздуха (136 городов);

· загрязнение и деградация почв;

· загрязнение поверхностных и подземных вод;

· US EPA

по химическим вредным веществам.

Большой объем информации имеется по загрязнению бассейна реки Теча и облучению населения в результате этого загрязнения.

WWW.MINATOM.NET - сайт ситуационно – кризисного центра Минатома РФ (СКЦ).

СКЦ осуществляет:

·               мониторинг радиационной и экологической обстановки объектов отрасли и районов их расположения;

·               мониторинг технического состояния объектов отрасли;

·               мониторинг финансово-экономической и других видов деятельности;

·               учет и контроль ядерных материалов;

·               мониторинг транспортировки ядерных материалов, ядерных боеприпасов и радиоактивных веществ;

·               обеспечение доступа предприятий отрасли к информационному фонду СКЦ.

WWW.GEOEXPERT.KIEV.UA - сайт Научно-инженерного центра радиогидрогеоэкологических полигонных исследований Национальной Академии Наук Украины.

"Геоэксперт" занимается следующими вопросами:

·               прогнозные расчеты фильтрации подземных вод (профильные, плановые, трехмерные задачи) в естественных и нарушенных условиях с использованием численных моделей;

·               оценки гидрогеологических и миграционных параметров по данным натурных наблюдений (решение обратных задач);

·               расчеты движения влаги и солей в почвогрунтах зоны аэрации (1, 2 - мерная постановка);

·               расчеты миграции техногенных загрязнителей (радионуклиды, тяжелые металлы) в почвах зоны аэрации и подземных водах;

·               расчеты разгрузки подземных вод в поверхностные водоемы (реки, водохранилища) и сопутствующие расчеты выноса загрязняющих веществ;

·               оценки рисков для здоровья в связи с загрязнением подземных вод;

·               вероятностные гидрогеологические прогнозы с учетом неопределенностей в параметрах моделей;

·               трехмерная компьютерная визуализация результатов моделирования и данных натурных гидрогеологических обследований;

·               представление результатов моделирования в формате геоинформационных систем;

·               организация специализированных баз данных геологической и гидрогеологической информации;

При расчетах "Геоэксперт" использует международно - апробированное программное обеспечение, в частности разработанные в США программы MODFLOW

и MT3D, которые стали своеобразным международным стандартом при расчетах фильтрации и миграции загрязняющих веществ в подземных водах. Для расчетов влагопереноса в ненасыщенной зоне почвогрунтов используется разработанная Геологическим надзором США программа VS2DTI, которая является одной из наиболее мощных программ данного класса.

Были проведены расчеты по прогнозированию фильтрации и миграции радионуклидов в подземных водах Чернобыльской зоны отчуждения, по моделированию утечек и водоема-охладителя Чернобыльской АЭС, по моделированию фильтрации и выщелачивания солей в основаниях гидротехнических сооружений, по моделированию режима движения влаги и солей на мелиорированных сельскохозяйственных землях, и по многим другим вопросам.

WWW.TYPHOON.MECOM.RU

- сайт Федерального Информационно-аналитического Центра Росгидромета (ФИАЦ), который является Региональным специализированным метеорологическим центром Всемирной Метеорологической Организации (РСМЦ ВМО) со специализацией деятельности в области обеспечения продукцией моделей атмосферного переноса при реагировании на чрезвычайные экологические ситуации.

Центр выполняет функции главного информационно-управляющего центра Росгидромета в составе функциональной подсистемы РСЧС и Единой государственной автоматизированной системы контроля радиационной обстановки (ЕГАСКРО) на территории Российской Федерации. В режиме повседневной деятельности ФИАЦ ведет сбор, обработку и хранение данных о состоянии радиационного и химического загрязнения окружающей природной среды на территории Российской Федерации. На сайте ежемесячно размещаются справки о радиоактивном загрязнении атмосферы на территории России и о радиационной обстановке вокруг радиационно-опасных объектов на территории Российской Федерации.

Из анализа экологических сайтов в ИНТЕРНЕТ

можно сделать следующие выводы:

1.      Большинство сайтов экологической направленности содержат информацию о состоянии ядерной безопасности в атомной отрасли России, положении с сохранностью ядерного оружия, сообщения об экологических форумах различного уровня.

2.      Существуют несколько близких к тематике проекта сайтов, содержащих информацию о радиационном загрязнении подземных вод.

3.      Необходимо налаживание контактов с разработчиками вышеперечисленных сайтов для совместных действий по популяризации экологической тематики в ИНТЕРНЕТ.

Литература к разделу

1. Петров В., М.Леспинас Изучение условий миграции загрязнителей в вадозной зоне: перспективы международного сотрудничества. Университет Анри Пуанкаре, Вандуврле-Нанси, Франция.

2. Полубаринова-Кочина П.Я. Теория движения грунтовых вод. Москва, 1977.

3. Павлоцкая Ф.И. «Миграция радиоактивных продуктов глобальных выпадений в почвах», Атомиздат, 1979, стр.18.

4. БЭС, М., Советская энциклопедия, 1975, т.20, стр.1156.

5. Куликов Н.В. «Континентальная радиоэкология», М., Наука, 1975, стр.104.

6. Дричко В.Ф. Поведение в природной среде тяжелых естественных радионуклидов. С/х Радиоэкология. М. Экология. 1986, стр.98.

7. Гаррелс Р.М. Некоторые термодинамические соотношения между соединениями урана и из связь с окислительными состояниями урановых руд. В сборнике: «Термодинамика геохимических процессов». М., Изд-во Иностр.лит., 1960, стр.207-222.

8. Борисов В.Н., Безденежных В.С., Овчинников Н.А. и др. «Разработка технологии очистки воды и почвы от радионуклидов и ионов тяжелых металлов», Технический отчет по проекту МНТЦ №16, Снежинск, 1997, стр.12.

9. Корнилович Б.Ю. «Влияние фульвокислот на взаимодействие радионуклидов с глинистыми компонентами почв», Радиохимия, 2000, т.42, № 2, стр.176.

10. Thortwait C.W., Mather J.R., Nakamura J.K. Science, 1963, v.131, №3406, p.1015.

11. Miller J.R., Reitemier R.F. Soil Sci. Soc. America Proc., 1960, v.27, №N1, p.141.

12. С/х Радиоэкология М. Экология, 1991, стр.30.

13. Кац.Дж., Сиборг Г. «Химия актиноидов», М., 1991, т.1, стр.248.

14. Никольский Б.П. Успехи химии. 1978, №10.

15. Sposito G. The Surface Chemistry of Soils. New Yofk: Oxford Univ.

Литература к разделу

1. Соколов Л.В., Симонова К.И., Шестаков А.А., Широковская О.С. Методические исследования для одномерных численных расчетов распространения загрязнения в пористой среде. Препринт №92, РФЯЦ-ВНИИТФ, Снежинск, 1996.

2. Шестаков А.А. Исследование возникновения осцилляций при решении одномерного уравнения миграции. Препринт №100, РФЯЦ-ВНИИТФ, Снежинск, 1996.

3. Соколов Л.В., Чернов В.В., Шестаков А.А. и др. Двумерная методика численного решения системы уравнений, описывающих распространение загрязнения в пористой среде. Препринт №104, РФЯЦ-ВНИИТФ, Снежинск, 1996.

4. Гаджиев А.Д., Соколов Л.В., Шестаков А.А. и др. Методика ‘РОМБ’ для численного решения трехмерного уравнения миграции радионуклидов в подземных водах на произвольных шестигранных сетках. Препринт №117, РФЯЦ-ВНИИТФ, Снежинск, 1997.

5. Голубкина О.В., Соколов Л.В., Филимонцев Г.А., Шестаков А.А. Численное сравнение методики МИФ и методики MT3D при решении трехмерного уравнения миграции. Препринт №118, РФЯЦ-ВНИИТФ, Снежинск, 1997.

6. Гаджиев А.Д., Филимонцев Г.А., Шестаков А.А. Методика МИФ для численного решения трехмерного уравнения миграции радионуклидов в подземных водах на произвольных шестигранных сетках. Препринт №126, РФЯЦ-ВНИИТФ, Снежинск, 1998.

7. Комоско В.В., Симоненко В.А., Шестаков А.А. и др. Математическое моделирование распространения загрязнения в подземных водах района озера Карачай. Препринт №134, РФЯЦ-ВНИИТФ, Снежинск, 1998.

8. Ивашкин Н.В., Петровцев А.В., Шестаков А.А. и др. Численное моделирование изменения состояния геологической среды и миграция радионуклидов в период до 10000 лет при глубинном захоронении. Препринт №133, РФЯЦ-ВНИИТФ, Снежинск, 1998.

9. Ивашкин Н.В., Петровцев А.В., Шестаков А.А. и др. Численное моделирование изменения состояния геологической среды и миграция радионуклидов в период до 10000 лет при глубинном захоронении.

Литература к разделу

1. Андерсон С.Р., Халлет Б. Общая модель переноса частиц ветром // Вашингтон, 98195.

2. Глазунов Г.П., Гендугов В.М. Механизмы ветровой эрозии почв // Почвоведение, 2001, №6.

3. Нигматулин Р.И. Основы механики гетерогенных сред // М.: Наука, 1978.

4. Рахматулин Х.А. Основы газодинамики взаимопроникающих движений сжимаемых сред // ПММ, 1956, Т.20, вып.2.

Математическая программа МИФ для описания распространения радона

Для описания процесса распространения загрязнения в подземных водах может быть использована созданная в Российском Федеральном Ядерном Центре численная методика МИФ. Методика МИФ предназначена для решения трехмерных уравнений миграции и фильтрации на произвольных шестигранных сетках. Методика располагает набором консервативных разностных схем, позволяющих получать монотонные решения для различных классов задач. Это, во-первых, многопараметрическая ДС-схема [1,2] второго порядка аппроксимации по пространству. Во-вторых, это диссипативная схема ‘РОМБ’ [3], позволяющая улучшать точность результатов за счет введения диссипативных поправок.

При использовании схем второго порядка точности в численном решении могут возникать осцилляции. В работе [2] проведено исследование возникновения осцилляций методом дифференциального приближения. Рассмотрено возникновение осцилляций как в однородной, так и в неоднородной средах. В однородной среде осцилляции не возникают при выполнении ограничений на параметр Пекле. В неоднородной среде осцилляции могут возникать даже при выполнении этих ограничений. Анализ прогоночных коэффициентов позволил построить устойчивую к таким осцилляциям аппроксимацию уравнения миграции. При рассмотрении трехточечного аналога ДС-схем получено обобщенное условие Куранта, которое в нелинейном случае при разрывах в скоростях фильтрационного потока может приводить к ограничениям на шаг по времени. Здесь же исследовано возникновение осцилляций при моделировании граничных условий и приведены результаты численных расчетов двух модельных задач, где рассмотрены среды с различными скоростями фильтрации и пористостью.

В работе [4] рассмотрено применение ДС-схемы для решения трехмерного уравнения миграции радионуклидов в подземных водах на произвольных шестигранных сетках. В данной работе сделана попытка улучшить монотонные свойства разностных схем второго порядка аппроксимации по пространству, применяемых для решения уравнения миграции радионуклидов, с помощью использования диссипативной разностной схемы.

В работе [5] на ряде модельных задач производится сравнение методики МИФ с методикой MT3D при решении трехмерного уравнения миграции. Методика MT3D, использующая смешанный эйлерово-лагранжевый подход для трехмерного уравнения миграции, широко используется в США при решении задач радиоактивного загрязнения среды. Результаты, полученные по различным методикам близки между собой, но методика МИФ дает более монотонное распределение радиоактивности в пространстве при решении трехмерных задач.

Методика МИФ разрабатывалась при поддержке проекта МНТЦ №51 ‘Создание и проверка модели для расчета миграции радиоактивности в подземных водах’ (1995-1998 г.г.). В данном проекте она применялась для описания распространения загрязнения вокруг озера Карачай, которое является крупнейшим в мире открытым хранилищем жидких радиоактивных отходов [6,7]. Численные результаты дали хорошее согласие с результатами непосредственных измерений в наблюдательных скважинах. Форма и объём ореолов загрязнения, полученных при моделировании миграции нейтральных стабильных компонентов, соответствуют реальному распространению ореолов, зафиксированным по данным режимных наблюдений.

В дальнейшем методика МИФ использовалась в проекте МНТЦ №793 (1997-1998 г.г.) ‘Экспериментальное и теоретическое исследование химических и физических свойств горных пород как естественного барьера при захоронении радиоактивных отходов’. Методика применялась для численного моделирования изменения состояния геологической среды и миграции радионуклидов в период до 10000 лет при глубинном захоронении радиоактивных отходов [8,9]. В данном проекте были разработаны физико-математические модели для расчетов процессов, сопровождающих глубинное захоронение отработанного топлива АЭС с реактором типа РБМК-1000, с целью прогнозирования состояния геологической среды в зоне захоронения и распределения концентраций радионуклидов на длительный период времени. Было выяснено, что в окружающей горной породе имеет место миграция плутония преимущественно в направлении к земной поверхности со скоростью движения головного фронта, примерно 0.015 м/год, и фоновые уровни альфа-загрязнения вблизи поверхности достигаются спустя 40 000 лет после захоронения.

Таким образом, с точки зрения радиационной опасности, забивочный комплекс является наиболее критичным элементом системы захоронения и предотвращение раннего выхода радиоактивности в окружающую среду требует принятия дополнительных мер по увеличению стойкости контейнера с ТВС к выщелачиванию.

В проекте МНТЦ №KR-72 ‘Разработка научных основ и комплексное изучение радиационной и иной опасности хвостохранилищ Северного Кыргызстана, аккумулирующих радиоактивные изотопы и сопутствующие токсичные металлы’ (1997-2000 г.г.) [10-13] методика МИФ применялась для установления закономерностей пространственного распределения вокруг хвостохранилища радиоактивных и других токсичных ингредиентов вследствии их миграции от Кара-Балтинского горнорудного комбината в пределах Чуйской долины. Трудности состояли в том, что в подземных и поверхностных водах вокруг хвостохранилища необходимо определить техногенную и естественную, не связанную с хвостохранилищем, составляющие. Соотношение между ними меняется в пространстве по мере разбавления токсичных вод хвостохранилища обычными природными водами. Были построены экологические карты сопредельных с хвостохранилищем территорий с выделением экологически неблагоприятных участков различной степени опасности и даны рекомендации по снижению радиоизотопной и иной экологической опасности от хвостохранилища.

В проекте МНТЦ №KR-187.2 'Создание автоматизированной системы радонового мониторинга и разработка рекомендаций по её использованию в качестве информативного предвестника землетрясений Северного Тянь-Шаня (Кыргызская Республика)’ (2001-2003 г.г.) [14] методика МИФ применялась для моделирования миграции радона в трещиновато-пористой среде в условиях принудительной откачки воздуха из приповерхностного слоя почвы. Горные породы, в общем случае, являются средами с двойной пористостью, емкость которых определяется объемом слабо проводящих поровых блоков, а проницаемость – объемом трещин (в предельных случаях, когда блоки либо монолитны, либо, наоборот, сильно раздроблены и многие поры становятся проводящими, среду можно считать чисто пористой).Соответственно, основное количество радона хранится в порах, а распространяться он может лишь по проводящим каналам – трещинам. В этом проекте сформулирована и программно реализована двумерная осесимметричная модель фильтрации и миграции радона в трещиновато-пористой среде, проведено тестирование в приближениях одномерной и двумерной геометрий.

В данном проекте методика МИФ применялась для изучения переноса радона с поверхности хвостохранилища.